LogPoissonNoise

class deepinv.physics.LogPoissonNoise(N0=1024.0, mu=0.02, rng: Generator | None = None)

Bases: NoiseModel

Log-Poisson noise \(y = \frac{1}{\mu} \log(\frac{\mathcal{P}(\exp(-\mu x) N_0)}{N_0})\).

This noise model is mostly used for modelling the noise for (low dose) computed tomography measurements. Here, N0 describes the average number of measured photons. It acts as a noise-level parameter, where a larger value of N0 corresponds to a lower strength of the noise. The value mu acts as a normalization constant of the forward operator. Consequently it should be chosen antiproportionally to the image size.

For more details on the interpretation of the parameters for CT measurements, we refer to the paper “LoDoPaB-CT, a benchmark dataset for low-dose computed tomography reconstruction”.

Parameters:

• N0 (float) –

  number of photons

  ---

• mu (float) – normalization constant

• rng (torch.Generator (Optional)) – a pseudorandom random number generator for the parameter generation.

Examples:

Adding LogPoisson noise to a physics operator by setting the noise_model attribute of the physics operator:

>>> from deepinv.physics import Denoising, LogPoissonNoise
>>> import torch
>>> physics = Denoising()
>>> physics.noise_model = LogPoissonNoise()
>>> x = torch.rand(1, 1, 2, 2)
>>> y = physics(x)

forward(x, mu=None, N0=None, seed: int | None = None, **kwargs)

Adds the noise to measurements x

Parameters:

• x (torch.Tensor) – measurements

• mu (None, float, torch.Tensor) – number of photons. If not None, it will overwrite the current number of photons.

• N0 (None, float, torch.Tensor) – normalization constant. If not None, it will overwrite the current normalization constant.

• seed (int) – the seed for the random number generator, if rng is provided.

Returns:

noisy measurements

update_parameters(mu=None, N0=None, **kwargs)

Updates the number of photons and normalization constant.

Parameters:

• mu (float, torch.Tensor) – number of photons.

• N0 (float, torch.Tensor) – normalization constant.

Examples using LogPoissonNoise:

Patch priors for limited-angle computed tomography

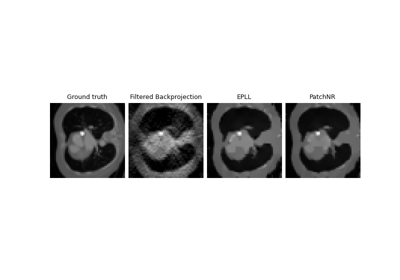
Patch priors for limited-angle computed tomography