Prior
- class deepinv.optim.Prior(g=None)[source]
Bases:
ModulePrior term \(\reg{x}\).
This is the base class for the prior term \(\reg{x}\). Similarly to the
deepinv.optim.DataFidelity()class, this class comes with methods for computing \(\operatorname{prox}_{g}\) and \(\nabla \regname\). To implement a custom prior, for an explicit prior, overwrite \(\regname\) (do not forget to specify self.explicit_prior = True)This base class is also used to implement implicit priors. For instance, in PnP methods, the method computing the proximity operator is overwritten by a method performing denoising. For an implicit prior, overwrite grad or prox.
Note
The methods for computing the proximity operator and the gradient of the prior rely on automatic differentiation. These methods should not be used when the prior is not differentiable, although they will not raise an error.
- Parameters:
g (callable) – Prior function \(g(x)\).
- forward(x, *args, **kwargs)[source]
Computes the prior \(g(x)\).
- Parameters:
x (torch.Tensor) – Variable \(x\) at which the prior is computed.
- Returns:
(torch.tensor) prior \(g(x)\).
- g(x, *args, **kwargs)[source]
Computes the prior \(g(x)\).
- Parameters:
x (torch.Tensor) – Variable \(x\) at which the prior is computed.
- Returns:
(torch.tensor) prior \(g(x)\).
- grad(x, *args, **kwargs)[source]
Calculates the gradient of the prior term \(\regname\) at \(x\). By default, the gradient is computed using automatic differentiation.
- Parameters:
x (torch.Tensor) – Variable \(x\) at which the gradient is computed.
- Returns:
(torch.tensor) gradient \(\nabla_x g\), computed in \(x\).
- prox(x, *args, gamma=1.0, stepsize_inter=1.0, max_iter_inter=50, tol_inter=0.001, **kwargs)[source]
Calculates the proximity operator of \(\regname\) at \(x\). By default, the proximity operator is computed using internal gradient descent.
- Parameters:
x (torch.Tensor) – Variable \(x\) at which the proximity operator is computed.
gamma (float) – stepsize of the proximity operator.
stepsize_inter (float) – stepsize used for internal gradient descent
max_iter_inter (int) – maximal number of iterations for internal gradient descent.
tol_inter (float) – internal gradient descent has converged when the L2 distance between two consecutive iterates is smaller than tol_inter.
- Returns:
(torch.tensor) proximity operator \(\operatorname{prox}_{\gamma g}(x)\), computed in \(x\).
- prox_conjugate(x, *args, gamma=1.0, lamb=1.0, **kwargs)[source]
Calculates the proximity operator of the convex conjugate \((\lambda g)^*\) at \(x\), using the Moreau formula.
::Warning:: Only valid for convex \(\regname\)
- Parameters:
x (torch.Tensor) – Variable \(x\) at which the proximity operator is computed.
gamma (float) – stepsize of the proximity operator.
lamb (float) – math:lambda parameter in front of \(f\)
- Returns:
(torch.tensor) proximity operator \(\operatorname{prox}_{\gamma \lambda g)^*}(x)\), computed in \(x\).
Examples using Prior:
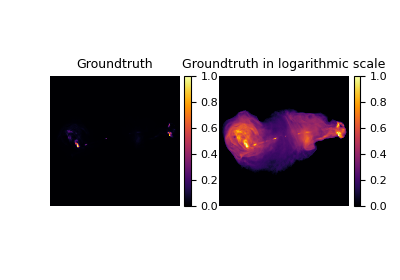
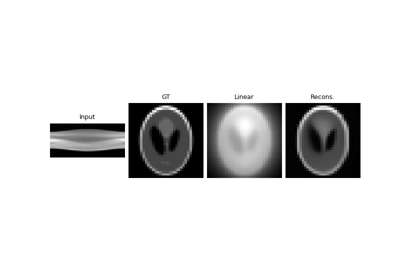
Random phase retrieval and reconstruction methods.
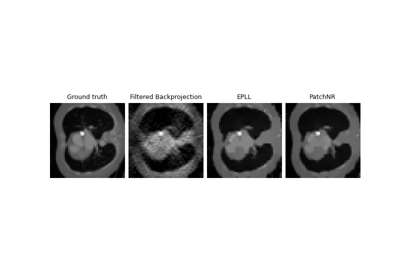
Patch priors for limited-angle computed tomography
Regularization by Denoising (RED) for Super-Resolution.
PnP with custom optimization algorithm (Condat-Vu Primal-Dual)
Learned Iterative Soft-Thresholding Algorithm (LISTA) for compressed sensing
Deep Equilibrium (DEQ) algorithms for image deblurring
Unfolded Chambolle-Pock for constrained image inpainting