Note

Go to the end to download the full example code.

Random phase retrieval and reconstruction methods.#

This example shows how to create a random phase retrieval operator and generate phaseless measurements from a given image. The example showcases 4 different reconstruction methods to recover the image from the phaseless measurements:

  1. Gradient descent with random initialization;

  2. Spectral methods;

  3. Gradient descent with spectral methods initialization;

  4. Gradient descent with PnP denoisers.

General setup#

import deepinv as dinv
from pathlib import Path
import torch
import matplotlib.pyplot as plt
from deepinv.models import DRUNet
from deepinv.optim.data_fidelity import L2
from deepinv.optim.prior import PnP, Zero
from deepinv.optim.optimizers import optim_builder
from deepinv.utils.demo import load_url_image, get_image_url
from deepinv.utils.plotting import plot
from deepinv.optim.phase_retrieval import (
    correct_global_phase,
    cosine_similarity,
    spectral_methods,
)
from deepinv.models.complex import to_complex_denoiser

BASE_DIR = Path(".")
RESULTS_DIR = BASE_DIR / "results"
# Set global random seed to ensure reproducibility.
torch.manual_seed(0)

device = dinv.utils.get_freer_gpu() if torch.cuda.is_available() else "cpu"

Load image from the internet#

We use the standard test image “Shepp–Logan phantom”.

# Image size
img_size = 32
url = get_image_url("SheppLogan.png")
# The pixel values of the image are in the range [0, 1].
x = load_url_image(
    url=url, img_size=img_size, grayscale=True, resize_mode="resize", device=device
)
print(x.min(), x.max())

tensor(0.) tensor(0.7412)

Visualization#

We use the customized plot() function in deepinv to visualize the original image.

plot(x, titles="Original image")
Original image

Signal construction#

We use the original image as the phase information for the complex signal. The original value range is [0, 1], and we map it to the phase range [-pi/2, pi/2].

x_phase = torch.exp(1j * x * torch.pi - 0.5j * torch.pi)

# Every element of the signal should have unit norm.
assert torch.allclose(x_phase.real**2 + x_phase.imag**2, torch.tensor(1.0))

Measurements generation#

Create a random phase retrieval operator with an oversampling ratio (measurements/pixels) of 5.0, and generate measurements from the signal with additive Gaussian noise.

# Define physics information
oversampling_ratio = 5.0
img_shape = x.shape[1:]
m = int(oversampling_ratio * torch.prod(torch.tensor(img_shape)))
n_channels = 1  # 3 for color images, 1 for gray-scale images

# Create the physics
physics = dinv.physics.RandomPhaseRetrieval(
    m=m,
    img_shape=img_shape,
    device=device,
)

# Generate measurements
y = physics(x_phase)

Reconstruction with gradient descent and random initialization#

First, we use the function deepinv.optim.L2 as the data fidelity function, and the class deepinv.optim.optim_iterators.GDIteration as the optimizer to run a gradient descent algorithm. The initial guess is a random complex signal.

data_fidelity = L2()
prior = Zero()
iterator = dinv.optim.optim_iterators.GDIteration()
# Parameters for the optimizer, including stepsize and regularization coefficient.
optim_params = {"stepsize": 0.06, "lambda": 1.0, "g_param": []}
num_iter = 1000

# Initial guess
x_phase_gd_rand = torch.randn_like(x_phase)

loss_hist = []

for _ in range(num_iter):
    res = iterator(
        {"est": (x_phase_gd_rand,), "cost": 0},
        cur_data_fidelity=data_fidelity,
        cur_prior=prior,
        cur_params=optim_params,
        y=y,
        physics=physics,
    )
    x_phase_gd_rand = res["est"][0]
    loss_hist.append(data_fidelity(x_phase_gd_rand, y, physics).cpu())

print("initial loss:", loss_hist[0])
print("final loss:", loss_hist[-1])
# Plot the loss curve
plt.plot(loss_hist)
plt.yscale("log")
plt.title("loss curve (gradient descent with random initialization)")
plt.show()
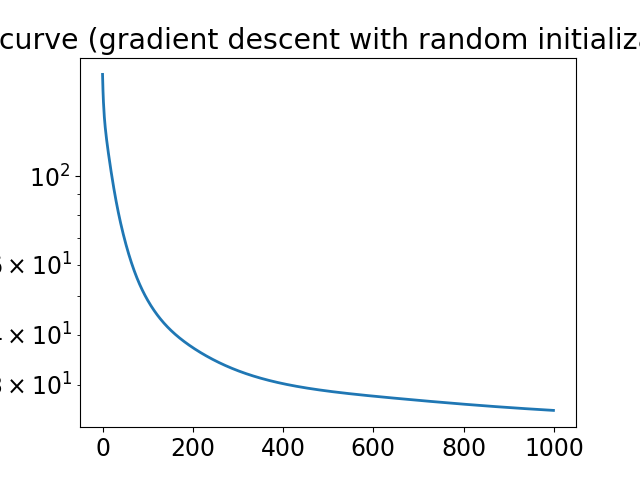
loss curve (gradient descent with random initialization)
initial loss: tensor([190.4569])
final loss: tensor([28.0710])

Phase correction and signal reconstruction#

The solution of the optimization algorithm x_est may be any phase-shifted version of the original complex signal x_phase, i.e., x_est = a * x_phase where a is an arbitrary unit norm complex number. Therefore, we use the function deepinv.optim.phase_retrieval.correct_global_phase to correct the global phase shift of the estimated signal x_est to make it closer to the original signal x_phase. We then use torch.angle to extract the phase information. With the range of the returned value being [-pi/2, pi/2], we further normalize it to be [0, 1]. This operation will later be done for all the reconstruction methods.

# correct possible global phase shifts
x_gd_rand = correct_global_phase(x_phase_gd_rand, x_phase)
# extract phase information and normalize to the range [0, 1]
x_gd_rand = torch.angle(x_gd_rand) / torch.pi + 0.5

plot([x, x_gd_rand], titles=["Signal", "Reconstruction"], rescale_mode="clip")
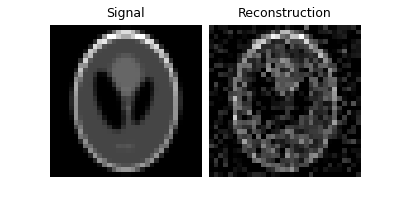
Signal, Reconstruction

Reconstruction with spectral methods#

Spectral methods deepinv.optim.phase_retrieval.spectral_methods offers a good initial guess on the original signal. Moreover, deepinv.physics.RandomPhaseRetrieval uses spectral methods as its default reconstruction method A_dagger, which we can directly call.

# Spectral methods return a tensor with unit norm.
x_phase_spec = physics.A_dagger(y, n_iter=300)

Phase correction and signal reconstruction#

# correct possible global phase shifts
x_spec = correct_global_phase(x_phase_spec, x_phase)
# extract phase information and normalize to the range [0, 1]
x_spec = torch.angle(x_spec) / torch.pi + 0.5
plot([x, x_spec], titles=["Signal", "Reconstruction"], rescale_mode="clip")
Signal, Reconstruction

Reconstruction with gradient descent and spectral methods initialization#

The estimate from spectral methods can be directly used as the initial guess for the gradient descent algorithm.

# Initial guess from spectral methods
x_phase_gd_spec = physics.A_dagger(y, n_iter=300)

loss_hist = []
for _ in range(num_iter):
    res = iterator(
        {"est": (x_phase_gd_spec,), "cost": 0},
        cur_data_fidelity=data_fidelity,
        cur_prior=prior,
        cur_params=optim_params,
        y=y,
        physics=physics,
    )
    x_phase_gd_spec = res["est"][0]
    loss_hist.append(data_fidelity(x_phase_gd_spec, y, physics).cpu())

print("intial loss:", loss_hist[0])
print("final loss:", loss_hist[-1])
plt.plot(loss_hist)
plt.yscale("log")
plt.title("loss curve (gradient descent with spectral initialization)")
plt.show()
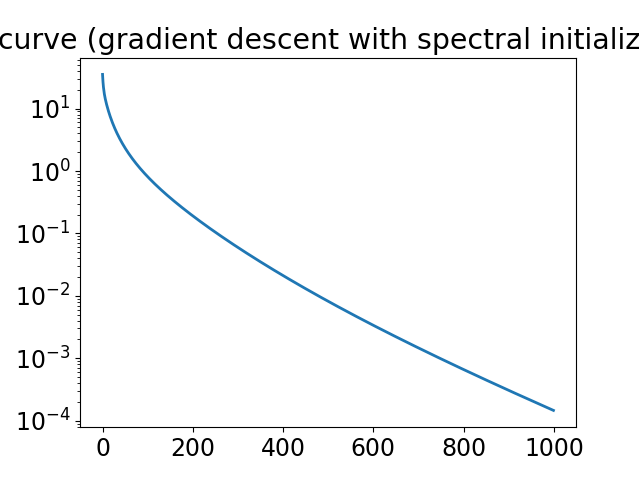
loss curve (gradient descent with spectral initialization)
intial loss: tensor([42.0413])
final loss: tensor([0.0034])

Phase correction and signal reconstruction#

# correct possible global phase shifts
x_gd_spec = correct_global_phase(x_phase_gd_spec, x_phase)
# extract phase information and normalize to the range [0, 1]
x_gd_spec = torch.angle(x_gd_spec) / torch.pi + 0.5
plot([x, x_gd_spec], titles=["Signal", "Reconstruction"], rescale_mode="clip")
Signal, Reconstruction

Reconstruction with gradient descent and PnP denoisers#

We can also use the Plug-and-Play (PnP) framework to incorporate denoisers as regularizers in the optimization algorithm. We use a deep denoiser as the prior, which is trained on a large dataset of natural images.

# Load the pre-trained denoiser
denoiser = DRUNet(
    in_channels=n_channels,
    out_channels=n_channels,
    pretrained="download",  # automatically downloads the pretrained weights, set to a path to use custom weights.
    device=device,
)
# The original denoiser is designed for real-valued images, so we need to convert it to a complex-valued denoiser for phase retrieval problems.
denoiser_complex = to_complex_denoiser(denoiser, mode="abs_angle")

# Algorithm parameters
data_fidelity = L2()
prior = PnP(denoiser=denoiser_complex)
params_algo = {"stepsize": 0.30, "g_param": 0.04}
max_iter = 100
early_stop = True
verbose = True

# Instantiate the algorithm class to solve the IP problem.
model = optim_builder(
    iteration="PGD",
    prior=prior,
    data_fidelity=data_fidelity,
    early_stop=early_stop,
    max_iter=max_iter,
    verbose=verbose,
    params_algo=params_algo,
)

# Run the algorithm
x_phase_pnp, metrics = model(y, physics, x_gt=x_phase, compute_metrics=True)

Downloading: "https://huggingface.co/deepinv/drunet/resolve/main/drunet_deepinv_gray_finetune_26k.pth?download=true" to /home/runner/.cache/torch/hub/checkpoints/drunet_deepinv_gray_finetune_26k.pth

  0%|          | 0.00/125M [00:00<?, ?B/s]
  1%|          | 1.12M/125M [00:00<00:12, 10.5MB/s]
  2%|▏         | 2.12M/125M [00:00<00:12, 10.3MB/s]
  3%|▎         | 3.25M/125M [00:00<00:11, 10.9MB/s]
  4%|▎         | 4.38M/125M [00:00<00:12, 10.3MB/s]
  4%|▍         | 5.38M/125M [00:00<00:12, 10.3MB/s]
  5%|▌         | 6.38M/125M [00:00<00:11, 10.4MB/s]
  6%|▌         | 7.38M/125M [00:00<00:11, 10.3MB/s]
  7%|▋         | 8.38M/125M [00:00<00:11, 10.3MB/s]
  8%|▊         | 9.38M/125M [00:00<00:11, 10.4MB/s]
  8%|▊         | 10.5M/125M [00:01<00:11, 10.8MB/s]
  9%|▉         | 11.6M/125M [00:01<00:11, 10.3MB/s]
 10%|█         | 12.6M/125M [00:01<00:11, 10.3MB/s]
 11%|█         | 13.6M/125M [00:01<00:11, 10.4MB/s]
 12%|█▏        | 14.6M/125M [00:01<00:11, 10.4MB/s]
 13%|█▎        | 15.6M/125M [00:01<00:11, 10.3MB/s]
 13%|█▎        | 16.6M/125M [00:01<00:10, 10.3MB/s]
 14%|█▍        | 17.6M/125M [00:01<00:10, 10.3MB/s]
 15%|█▍        | 18.6M/125M [00:01<00:10, 10.3MB/s]
 16%|█▌        | 19.6M/125M [00:01<00:10, 10.3MB/s]
 17%|█▋        | 20.6M/125M [00:02<00:10, 10.3MB/s]
 17%|█▋        | 21.6M/125M [00:02<00:10, 10.3MB/s]
 18%|█▊        | 22.8M/125M [00:02<00:09, 10.7MB/s]
 19%|█▉        | 23.9M/125M [00:02<00:10, 10.2MB/s]
 20%|█▉        | 24.9M/125M [00:02<00:10, 10.2MB/s]
 21%|██        | 25.9M/125M [00:02<00:10, 10.2MB/s]
 22%|██▏       | 27.1M/125M [00:02<00:09, 10.4MB/s]
 23%|██▎       | 28.2M/125M [00:02<00:09, 10.7MB/s]
 24%|██▎       | 29.4M/125M [00:02<00:09, 10.3MB/s]
 24%|██▍       | 30.4M/125M [00:03<00:09, 10.3MB/s]
 25%|██▌       | 31.4M/125M [00:03<00:09, 10.4MB/s]
 26%|██▌       | 32.4M/125M [00:03<00:09, 10.4MB/s]
 27%|██▋       | 33.5M/125M [00:03<00:08, 10.8MB/s]
 28%|██▊       | 34.6M/125M [00:03<00:09, 10.3MB/s]
 29%|██▊       | 35.6M/125M [00:03<00:08, 10.4MB/s]
 29%|██▉       | 36.6M/125M [00:03<00:08, 10.4MB/s]
 30%|███       | 37.6M/125M [00:03<00:08, 10.4MB/s]
 31%|███       | 38.6M/125M [00:03<00:08, 10.4MB/s]
 32%|███▏      | 39.6M/125M [00:03<00:08, 10.4MB/s]
 33%|███▎      | 40.8M/125M [00:04<00:08, 10.8MB/s]
 34%|███▎      | 41.9M/125M [00:04<00:08, 10.3MB/s]
 34%|███▍      | 42.9M/125M [00:04<00:08, 10.4MB/s]
 35%|███▌      | 43.9M/125M [00:04<00:08, 10.4MB/s]
 36%|███▌      | 44.9M/125M [00:04<00:08, 10.4MB/s]
 37%|███▋      | 45.9M/125M [00:04<00:07, 10.4MB/s]
 38%|███▊      | 46.9M/125M [00:04<00:07, 10.4MB/s]
 38%|███▊      | 47.9M/125M [00:04<00:07, 10.4MB/s]
 39%|███▉      | 48.9M/125M [00:04<00:07, 10.4MB/s]
 40%|████      | 49.9M/125M [00:05<00:07, 10.4MB/s]
 41%|████      | 50.9M/125M [00:05<00:07, 10.4MB/s]
 42%|████▏     | 51.9M/125M [00:05<00:07, 10.4MB/s]
 42%|████▏     | 52.9M/125M [00:05<00:07, 10.4MB/s]
 43%|████▎     | 53.9M/125M [00:05<00:07, 10.4MB/s]
 44%|████▍     | 54.9M/125M [00:05<00:07, 10.4MB/s]
 45%|████▍     | 56.0M/125M [00:05<00:06, 10.8MB/s]
 46%|████▌     | 57.1M/125M [00:05<00:06, 10.3MB/s]
 47%|████▋     | 58.1M/125M [00:05<00:06, 10.3MB/s]
 47%|████▋     | 59.1M/125M [00:05<00:06, 10.3MB/s]
 48%|████▊     | 60.2M/125M [00:06<00:06, 10.7MB/s]
 49%|████▉     | 61.4M/125M [00:06<00:06, 10.3MB/s]
 50%|█████     | 62.4M/125M [00:06<00:06, 10.3MB/s]
 51%|█████     | 63.4M/125M [00:06<00:06, 10.4MB/s]
 52%|█████▏    | 64.4M/125M [00:06<00:06, 10.3MB/s]
 52%|█████▏    | 65.4M/125M [00:06<00:06, 10.3MB/s]
 53%|█████▎    | 66.5M/125M [00:06<00:05, 10.7MB/s]
 54%|█████▍    | 67.6M/125M [00:06<00:05, 10.3MB/s]
 55%|█████▌    | 68.6M/125M [00:06<00:05, 10.2MB/s]
 56%|█████▌    | 69.8M/125M [00:07<00:05, 10.7MB/s]
 57%|█████▋    | 70.9M/125M [00:07<00:05, 10.3MB/s]
 58%|█████▊    | 71.9M/125M [00:07<00:05, 10.3MB/s]
 59%|█████▊    | 72.9M/125M [00:07<00:05, 10.2MB/s]
 59%|█████▉    | 73.9M/125M [00:07<00:05, 10.3MB/s]
 60%|██████    | 74.9M/125M [00:07<00:05, 10.3MB/s]
 61%|██████    | 75.9M/125M [00:07<00:04, 10.3MB/s]
 62%|██████▏   | 76.9M/125M [00:07<00:04, 10.3MB/s]
 63%|██████▎   | 78.0M/125M [00:07<00:04, 10.7MB/s]
 64%|██████▎   | 79.1M/125M [00:07<00:04, 10.3MB/s]
 64%|██████▍   | 80.1M/125M [00:08<00:04, 10.3MB/s]
 65%|██████▌   | 81.1M/125M [00:08<00:04, 10.3MB/s]
 66%|██████▌   | 82.1M/125M [00:08<00:04, 10.3MB/s]
 67%|██████▋   | 83.1M/125M [00:08<00:04, 10.3MB/s]
 68%|██████▊   | 84.1M/125M [00:08<00:04, 10.4MB/s]
 68%|██████▊   | 85.1M/125M [00:08<00:03, 10.4MB/s]
 69%|██████▉   | 86.1M/125M [00:08<00:03, 10.4MB/s]
 70%|███████   | 87.2M/125M [00:08<00:03, 10.8MB/s]
 71%|███████   | 88.4M/125M [00:08<00:03, 10.3MB/s]
 72%|███████▏  | 89.4M/125M [00:09<00:03, 10.3MB/s]
 73%|███████▎  | 90.5M/125M [00:09<00:03, 10.7MB/s]
 74%|███████▎  | 91.6M/125M [00:09<00:03, 10.3MB/s]
 74%|███████▍  | 92.6M/125M [00:09<00:03, 10.3MB/s]
 75%|███████▌  | 93.6M/125M [00:09<00:03, 10.3MB/s]
 76%|███████▌  | 94.6M/125M [00:09<00:03, 10.3MB/s]
 77%|███████▋  | 95.6M/125M [00:09<00:02, 10.3MB/s]
 78%|███████▊  | 96.6M/125M [00:09<00:02, 10.3MB/s]
 78%|███████▊  | 97.6M/125M [00:09<00:02, 10.3MB/s]
 79%|███████▉  | 98.6M/125M [00:09<00:02, 10.3MB/s]
 80%|████████  | 99.6M/125M [00:10<00:02, 10.3MB/s]
 81%|████████  | 101M/125M [00:10<00:02, 10.3MB/s]
 82%|████████▏ | 102M/125M [00:10<00:02, 10.3MB/s]
 83%|████████▎ | 103M/125M [00:10<00:02, 10.7MB/s]
 83%|████████▎ | 104M/125M [00:10<00:02, 10.3MB/s]
 84%|████████▍ | 105M/125M [00:10<00:02, 10.3MB/s]
 85%|████████▌ | 106M/125M [00:10<00:01, 10.3MB/s]
 86%|████████▌ | 107M/125M [00:10<00:01, 10.4MB/s]
 87%|████████▋ | 108M/125M [00:10<00:01, 10.4MB/s]
 87%|████████▋ | 109M/125M [00:10<00:01, 10.4MB/s]
 88%|████████▊ | 110M/125M [00:11<00:01, 10.4MB/s]
 89%|████████▉ | 111M/125M [00:11<00:01, 10.4MB/s]
 90%|████████▉ | 112M/125M [00:11<00:01, 10.8MB/s]
 91%|█████████ | 113M/125M [00:11<00:01, 10.4MB/s]
 92%|█████████▏| 114M/125M [00:11<00:01, 10.4MB/s]
 93%|█████████▎| 115M/125M [00:11<00:00, 10.8MB/s]
 93%|█████████▎| 116M/125M [00:11<00:00, 10.3MB/s]
 94%|█████████▍| 117M/125M [00:11<00:00, 10.4MB/s]
 95%|█████████▌| 118M/125M [00:11<00:00, 10.4MB/s]
 96%|█████████▌| 119M/125M [00:12<00:00, 10.4MB/s]
 97%|█████████▋| 120M/125M [00:12<00:00, 10.2MB/s]
 98%|█████████▊| 122M/125M [00:12<00:00, 10.7MB/s]
 98%|█████████▊| 123M/125M [00:12<00:00, 10.2MB/s]
 99%|█████████▉| 124M/125M [00:12<00:00, 10.3MB/s]
100%|██████████| 125M/125M [00:12<00:00, 10.4MB/s]

Phase correction and signal reconstruction#

# correct possible global phase shifts
x_pnp = correct_global_phase(x_phase_pnp, x_phase)
# extract phase information and normalize to the range [0, 1]
x_pnp = torch.angle(x_pnp) / (2 * torch.pi) + 0.5
plot([x, x_pnp], titles=["Signal", "Reconstruction"], rescale_mode="clip")
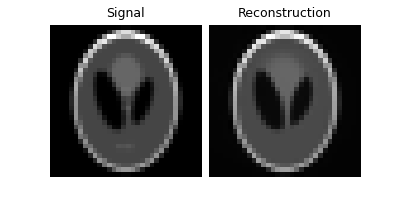
Signal, Reconstruction

Overall comparison#

We visualize the original image and the reconstructed images from the four methods. We further compute the PSNR (Peak Signal-to-Noise Ratio) scores (higher better) for every reconstruction and their cosine similarities with the original image (range in [0,1], higher better). In conclusion, gradient descent with random intialization provides a poor reconstruction, while spectral methods provide a good initial estimate which can later be improved by gradient descent to acquire the best reconstruction results. Besides, the PnP framework with a deep denoiser as the prior also provides a very good denoising results as it exploits prior information about the set of natural images.

imgs = [x, x_gd_rand, x_spec, x_gd_spec, x_pnp]
plot(
    imgs,
    titles=["Original", "GD random", "Spectral", "GD spectral", "PnP"],
    save_dir=RESULTS_DIR / "images",
    show=True,
    rescale_mode="clip",
)

# Compute metrics
print(
    f"GD Random reconstruction, PSNR: {dinv.metric.cal_psnr(x, x_gd_rand).item():.2f} dB; cosine similarity: {cosine_similarity(x_phase_gd_rand, x_phase).item():.3f}."
)
print(
    f"Spectral reconstruction, PSNR: {dinv.metric.cal_psnr(x, x_spec).item():.2f} dB; cosine similarity: {cosine_similarity(x_phase_spec, x_phase).item():.3f}."
)
print(
    f"GD Spectral reconstruction, PSNR: {dinv.metric.cal_psnr(x, x_gd_spec).item():.2f} dB; cosine similarity: {cosine_similarity(x_phase_gd_spec, x_phase).item():.3f}."
)
print(
    f"PnP reconstruction, PSNR: {dinv.metric.cal_psnr(x, x_pnp).item():.2f} dB; cosine similarity: {cosine_similarity(x_phase_pnp, x_phase).item():.3f}."
)
Original, GD random, Spectral, GD spectral, PnP
GD Random reconstruction, PSNR: 3.95 dB; cosine similarity: 0.201.
Spectral reconstruction, PSNR: 18.88 dB; cosine similarity: 0.902.
GD Spectral reconstruction, PSNR: 50.80 dB; cosine similarity: 1.000.
PnP reconstruction, PSNR: 13.83 dB; cosine similarity: 0.999.

Total running time of the script: (0 minutes 46.624 seconds)

Gallery generated by Sphinx-Gallery