Note
New to DeepInverse? Get started with the basics with the 5 minute quickstart tutorial..
Regularization by Denoising (RED) for Super-Resolution.#
Implementation of Romano et al.[1] using as plug-in denoiser the Gradient-Step Denoiser (GSPnP) Hurault et al.[2] which provides an explicit prior.
import deepinv as dinv
from pathlib import Path
import torch
from torch.utils.data import DataLoader
from deepinv.optim.data_fidelity import L2
from deepinv.optim.prior import RED
from deepinv.optim import PGD
from deepinv.training import test
from torchvision import transforms
from deepinv.utils.parameters import get_GSPnP_params
from deepinv.utils import load_dataset, load_degradation
Setup paths for data loading and results.#
BASE_DIR = Path(".")
DATA_DIR = BASE_DIR / "measurements"
RESULTS_DIR = BASE_DIR / "results"
DEG_DIR = BASE_DIR / "degradations"
# Set the global random seed from pytorch to ensure
# the reproducibility of the example.
torch.manual_seed(0)
device = dinv.utils.get_device()
Selected GPU 0 with 5015.25 MiB free memory
Load base image datasets and degradation operators.#
In this example, we use the Set3C dataset and a motion blur kernel from Levin et al.[3].
dataset_name = "set3c"
img_size = 256 if torch.cuda.is_available() else 32
operation = "super-resolution"
val_transform = transforms.Compose(
[transforms.CenterCrop(img_size), transforms.ToTensor()]
)
dataset = load_dataset(dataset_name, transform=val_transform)
# Generate the degradation operator.
kernel_index = 1
kernel_torch = load_degradation(
"kernels_12.npy", DEG_DIR / "kernels", index=kernel_index
)
kernel_torch = kernel_torch.unsqueeze(0).unsqueeze(
0
) # add batch and channel dimensions
# Use parallel dataloader if using a GPU to speed up training, otherwise, as all computes are on CPU, use synchronous dataloading.
num_workers = 4 if torch.cuda.is_available() else 0
factor = 2 # down-sampling factor
n_channels = 3 # 3 for color images, 1 for gray-scale images
n_images_max = 3 # Maximal number of images to restore from the input dataset
noise_level_img = 0.03 # Gaussian Noise standard deviation for the degradation
p = dinv.physics.Downsampling(
img_size=(n_channels, img_size, img_size),
factor=factor,
filter=kernel_torch,
device=device,
noise_model=dinv.physics.GaussianNoise(sigma=noise_level_img),
)
# Generate a dataset in a HDF5 folder in "{dir}/dinv_dataset0.h5'" and load it.
measurement_dir = DATA_DIR / dataset_name / operation
dinv_dataset_path = dinv.datasets.generate_dataset(
train_dataset=dataset,
test_dataset=None,
physics=p,
device=device,
save_dir=measurement_dir,
train_datapoints=n_images_max,
num_workers=num_workers,
)
dataset = dinv.datasets.HDF5Dataset(path=dinv_dataset_path, train=True)
kernels_12.npy degradation downloaded in degradations/kernels
Dataset has been saved at measurements/set3c/super-resolution/dinv_dataset0.h5
Setup the PnP algorithm. This involves in particular the definition of a custom prior class.#
We use the proximal gradient algorithm to solve the super-resolution problem with GSPnP.
# Parameters of the algorithm to solve the inverse problem
early_stop = True # Stop algorithm when convergence criteria is reached
crit_conv = "cost" # Convergence is reached when the difference of cost function between consecutive iterates is
# smaller than thres_conv
thres_conv = 1e-5
backtracking = True
batch_size = 1 # batch size for evaluation is necessarily 1 for early stopping and backtracking to work.
# load specific parameters for GSPnP
lambda_reg, sigma_denoiser, stepsize, max_iter = get_GSPnP_params(
operation, noise_level_img
)
# Select the data fidelity term
data_fidelity = L2()
# The GSPnP prior corresponds to a RED prior with an explicit `g`.
# We thus write a class that inherits from RED for this custom prior.
class GSPnP(RED):
r"""
Gradient-Step Denoiser prior.
"""
def __init__(self, *args, **kwargs):
super().__init__(*args, **kwargs)
self.explicit_prior = True
def forward(self, x, *args, **kwargs):
r"""
Computes the prior :math:`g(x)`.
:param torch.Tensor x: Variable :math:`x` at which the prior is computed.
:return: (torch.Tensor) prior :math:`g(x)`.
"""
return self.denoiser.potential(x, *args, **kwargs)
method = "GSPnP"
denoiser_name = "gsdrunet"
# Specify the Denoising prior
prior = GSPnP(denoiser=dinv.models.GSDRUNet(pretrained="download").to(device))
# we want to output the intermediate PGD update to finish with a denoising step.
def custom_output(X):
return X["est"][1]
# instantiate the algorithm class to solve the IP problem.
model = PGD(
prior=prior,
g_first=True,
data_fidelity=data_fidelity,
sigma_denoiser=sigma_denoiser,
lambda_reg=lambda_reg,
stepsize=stepsize,
early_stop=early_stop,
max_iter=max_iter,
crit_conv=crit_conv,
thres_conv=thres_conv,
backtracking=backtracking,
get_output=custom_output,
verbose=False,
)
# Set the model to evaluation mode. We do not require training here.
model.eval()
PGD(
(fixed_point): FixedPoint(
(iterator): PGDIteration(
(f_step): fStepPGD()
(g_step): gStepPGD()
)
)
(psnr): PSNR()
)
Evaluate the model on the problem.#
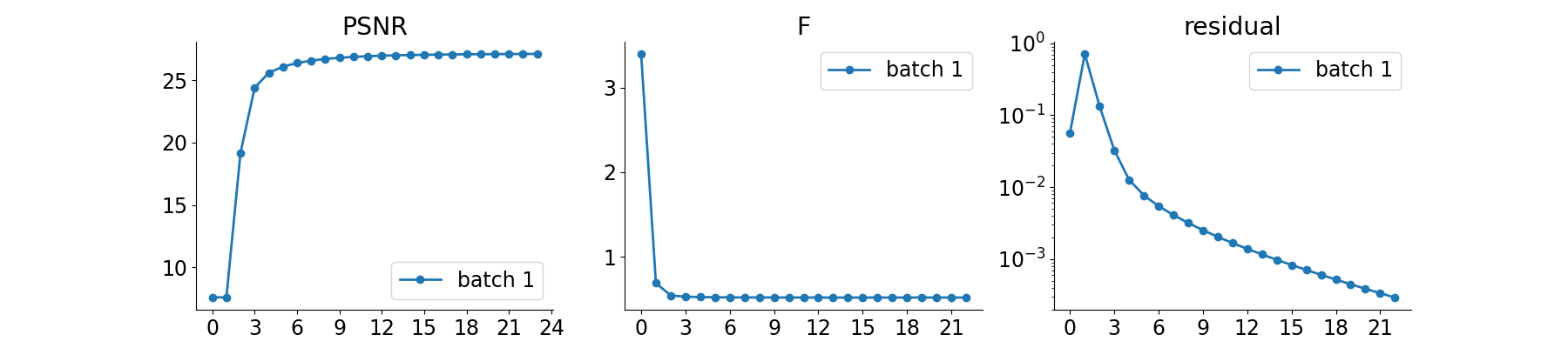
We evaluate the PnP algorithm on the test dataset, compute the PSNR metrics and plot reconstruction results.
save_folder = RESULTS_DIR / method / operation / dataset_name
plot_convergence_metrics = True # plot metrics. Metrics are saved in save_folder.
plot_images = True # plot images. Images are saved in save_folder.
dataloader = DataLoader(
dataset, batch_size=batch_size, num_workers=num_workers, shuffle=False
)
test(
model=model,
test_dataloader=dataloader,
physics=p,
device=device,
plot_images=plot_images,
save_folder=RESULTS_DIR / method / operation / dataset_name,
plot_convergence_metrics=plot_convergence_metrics,
verbose=True,
)
/local/jtachell/deepinv/deepinv/deepinv/training/trainer.py:549: UserWarning: Update progress bar frequency of 1 may slow down training on GPU. Consider setting freq_update_progress_bar > 1.
warnings.warn(
0%| | 0/3 [00:00<?, ?it/s]
Test: 0%| | 0/3 [00:00<?, ?it/s]
Test: 0%| | 0/3 [00:01<?, ?it/s, PSNR=28.4, PSNR no learning=7.88]
Test: 33%|███▎ | 1/3 [00:01<00:02, 1.33s/it, PSNR=28.4, PSNR no learning=7.88]
Test: 33%|███▎ | 1/3 [00:01<00:02, 1.33s/it, PSNR=28.4, PSNR no learning=7.88]
Test: 33%|███▎ | 1/3 [00:02<00:02, 1.33s/it, PSNR=28.6, PSNR no learning=6.39]
Test: 67%|██████▋ | 2/3 [00:02<00:01, 1.45s/it, PSNR=28.6, PSNR no learning=6.39]
Test: 67%|██████▋ | 2/3 [00:02<00:01, 1.45s/it, PSNR=28.6, PSNR no learning=6.39]
Test: 67%|██████▋ | 2/3 [00:03<00:01, 1.45s/it, PSNR=28.8, PSNR no learning=6.97]
Test: 100%|██████████| 3/3 [00:04<00:00, 1.48s/it, PSNR=28.8, PSNR no learning=6.97]
Test: 100%|██████████| 3/3 [00:04<00:00, 1.46s/it, PSNR=28.8, PSNR no learning=6.97]
Test results:
PSNR no learning: 6.969 +- 1.470
PSNR: 28.792 +- 0.293
{'PSNR no learning': 6.969034830729167, 'PSNR no learning_std': 1.4698685243410958, 'PSNR': 28.79173533121745, 'PSNR_std': 0.2930580657229568}
- References:
Total running time of the script: (0 minutes 6.745 seconds)