DataFidelity
- class deepinv.optim.DataFidelity(d=None)[source]
Bases:
ModuleData fidelity term \(\datafid{x}{y}=\distance{\forw{x}}{y}\).
This is the base class for the data fidelity term \(\datafid{x}{y} = \distance{\forw{x}}{y}\) where \(A\) is a linear or nonlinear operator, \(x\in\xset\) is a variable , \(y\in\yset\) is the observation and \(\distancename\) is a distance function.
>>> import torch >>> import deepinv as dinv >>> # define a loss function >>> data_fidelity = dinv.optim.L2() >>> >>> # Create a measurement operator >>> A = torch.Tensor([[2, 0], [0, 0.5]]) >>> A_forward = lambda v: A @ v >>> A_adjoint = lambda v: A.transpose(0, 1) @ v >>> >>> # Define the physics model associated to this operator >>> physics = dinv.physics.LinearPhysics(A=A_forward, A_adjoint=A_adjoint) >>> >>> # Define two points >>> x = torch.Tensor([[1], [4]]).unsqueeze(0) >>> y = torch.Tensor([[1], [1]]).unsqueeze(0) >>> >>> # Compute the loss :math:`f(x) = \datafid{A(x)}{y}` >>> data_fidelity(x, y, physics) tensor([1.0000]) >>> # Compute the gradient of :math:`f` >>> grad = data_fidelity.grad(x, y, physics) >>> >>> # Compute the proximity operator of :math:`f` >>> prox = data_fidelity.prox(x, y, physics, gamma=1.0)
Warning
All variables have a batch dimension as first dimension.
- Parameters:
d (callable) – data fidelity distance function \(\distance{u}{y}\). Outputs a tensor of size B, the size of the batch. Default: None.
- d(u, y, *args, **kwargs)[source]
Computes the data fidelity distance \(\distance{u}{y}\).
- Parameters:
u (torch.Tensor) – Variable \(u\) at which the distance function is computed.
y (torch.Tensor) – Data \(y\).
- Returns:
(torch.Tensor) data fidelity \(\distance{u}{y}\).
- forward(x, y, physics, *args, **kwargs)[source]
Computes the data fidelity term \(\datafid{x}{y} = \distance{\forw{x}}{y}\).
- Parameters:
x (torch.Tensor) – Variable \(x\) at which the data fidelity is computed.
y (torch.Tensor) – Data \(y\).
physics (deepinv.physics.Physics) – physics model.
- Returns:
(torch.Tensor) data fidelity \(\datafid{x}{y}\).
- grad(x, y, physics, *args, **kwargs)[source]
Calculates the gradient of the data fidelity term \(\datafidname\) at \(x\).
The gradient is computed using the chain rule:
\[\nabla_x \distance{\forw{x}}{y} = \left. \frac{\partial A}{\partial x} \right|_x^\top \nabla_u \distance{u}{y},\]where \(\left. \frac{\partial A}{\partial x} \right|_x\) is the Jacobian of \(A\) at \(x\), and \(\nabla_u \distance{u}{y}\) is computed using
grad_dwith \(u = \forw{x}\). The multiplication is computed using theA_vjpmethod of the physics.- Parameters:
x (torch.Tensor) – Variable \(x\) at which the gradient is computed.
y (torch.Tensor) – Data \(y\).
physics (deepinv.physics.Physics) – physics model.
- Returns:
(torch.Tensor) gradient \(\nabla_x \datafid{x}{y}\), computed in \(x\).
- grad_d(u, y, *args, **kwargs)[source]
Computes the gradient \(\nabla_u\distance{u}{y}\), computed in \(u\). Note that this is the gradient of \(\distancename\) and not \(\datafidname\). By default, the gradient is computed using automatic differentiation.
- Parameters:
u (torch.Tensor) – Variable \(u\) at which the gradient is computed.
y (torch.Tensor) – Data \(y\) of the same dimension as \(u\).
- Returns:
(torch.Tensor) gradient of \(d\) in \(u\), i.e. \(\nabla_u\distance{u}{y}\).
- prox(x, y, physics, *args, gamma=1.0, stepsize_inter=1.0, max_iter_inter=50, tol_inter=0.001, **kwargs)[source]
Calculates the proximity operator of \(\datafidname\) at \(x\).
- Parameters:
x (torch.Tensor) – Variable \(x\) at which the proximity operator is computed.
y (torch.Tensor) – Data \(y\).
physics (deepinv.physics.Physics) – physics model.
gamma (float) – stepsize of the proximity operator.
stepsize_inter (float) – stepsize used for internal gradient descent
max_iter_inter (int) – maximal number of iterations for internal gradient descent.
tol_inter (float) – internal gradient descent has converged when the L2 distance between two consecutive iterates is smaller than tol_inter.
- Returns:
(torch.Tensor) proximity operator \(\operatorname{prox}_{\gamma \datafidname}(x)\), computed in \(x\).
- prox_conjugate(x, y, physics, *args, gamma=1.0, lamb=1.0, **kwargs)[source]
Calculates the proximity operator of the convex conjugate \((\lambda \datafidname)^*\) at \(x\), using the Moreau formula.
Warning
This function is only valid for convex \(\datafidname\).
- Parameters:
x (torch.Tensor) – Variable \(x\) at which the proximity operator is computed.
y (torch.Tensor) – Data \(y\).
physics (deepinv.physics.Physics) – physics model.
gamma (float) – stepsize of the proximity operator.
lamb (float) – math:lambda parameter in front of \(f\)
- Returns:
(torch.Tensor) proximity operator \(\operatorname{prox}_{\gamma (\lambda \datafidname)^*}(x)\), computed in \(x\).
- prox_d(u, y, *args, gamma=1.0, stepsize_inter=1.0, max_iter_inter=50, tol_inter=0.001, **kwargs)[source]
Computes the proximity operator \(\operatorname{prox}_{\gamma\distance{\cdot}{y}}(u)\), computed in \(u\). Note that this is the proximity operator of \(\distancename\) and not \(\datafidname\). By default, the proximity operator is computed using internal gradient descent.
- Parameters:
u (torch.Tensor) – Variable \(u\) at which the proximity operator is computed.
y (torch.Tensor) – Data \(y\) of the same dimension as \(u\).
gamma (float) – stepsize of the proximity operator.
stepsize_inter (float) – stepsize used for internal gradient descent
max_iter_inter (int) – maximal number of iterations for internal gradient descent.
tol_inter (float) – internal gradient descent has converged when the L2 distance between two consecutive iterates is smaller than tol_inter.
- Returns:
(torch.Tensor) proximity operator \(\operatorname{prox}_{\gamma\distance{\cdot}{y}}(u)\).
- prox_d_conjugate(u, y, *args, gamma=1.0, lamb=1.0, **kwargs)[source]
Calculates the proximity operator of the convex conjugate \((\lambda \distancename)^*\) at \(u\), using the Moreau formula.
Warning
This function is only valid for convex \(\distancename\).
- Parameters:
u (torch.Tensor) – Variable \(u\) at which the proximity operator is computed.
y (torch.Tensor) – Data \(y\).
gamma (float) – stepsize of the proximity operator.
lamb (float) – math:lambda parameter in front of \(\distancename\)
- Returns:
(torch.Tensor) proximity operator \(\operatorname{prox}_{\gamma (\lambda \distancename)^*}(x)\), computed in \(x\).
Examples using DataFidelity:

Random phase retrieval and reconstruction methods.
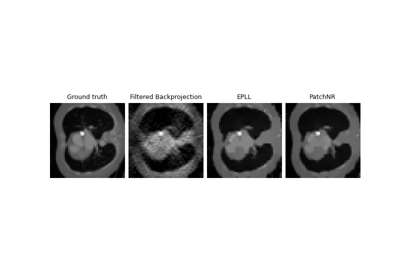
Patch priors for limited-angle computed tomography

Regularization by Denoising (RED) for Super-Resolution.

PnP with custom optimization algorithm (Condat-Vu Primal-Dual)

Learned Iterative Soft-Thresholding Algorithm (LISTA) for compressed sensing

Deep Equilibrium (DEQ) algorithms for image deblurring

Unfolded Chambolle-Pock for constrained image inpainting