Physics
- class deepinv.physics.Physics(A=<function Physics.<lambda>>, noise_model=<function Physics.<lambda>>, sensor_model=<function Physics.<lambda>>, max_iter=50, tol=0.001)[source]
Bases:
ModuleParent class for forward operators
It describes the general forward measurement process
\[y = N(A(x))\]where \(x\) is an image of \(n\) pixels, \(y\) is the measurements of size \(m\), \(A:\xset\mapsto \yset\) is a deterministic mapping capturing the physics of the acquisition and \(N:\yset\mapsto \yset\) is a stochastic mapping which characterizes the noise affecting the measurements.
- Parameters:
A (Callable) – forward operator function which maps an image to the observed measurements \(x\mapsto y\).
noise_model (Callable) – function that adds noise to the measurements \(N(z)\). See the noise module for some predefined functions.
sensor_model (Callable) – function that incorporates any sensor non-linearities to the sensing process, such as quantization or saturation, defined as a function \(\eta(z)\), such that \(y=\eta\left(N(A(x))\right)\). By default, the sensor_model is set to the identity \(\eta(z)=z\).
max_iter (int) – If the operator does not have a closed form pseudoinverse, the gradient descent algorithm is used for computing it, and this parameter fixes the maximum number of gradient descent iterations.
tol (float) – If the operator does not have a closed form pseudoinverse, the gradient descent algorithm is used for computing it, and this parameter fixes the absolute tolerance of the gradient descent algorithm.
- A(x, **kwargs)[source]
Computes forward operator \(y = A(x)\) (without noise and/or sensor non-linearities)
- Parameters:
x (torch.Tensor,list[torch.Tensor]) – signal/image
- Returns:
(torch.Tensor) clean measurements
- A_dagger(y, x_init=None)[source]
Computes an inverse as:
\[x^* \in \underset{x}{\arg\min} \quad \|\forw{x}-y\|^2.\]This function uses gradient descent to find the inverse. It can be overwritten by a more efficient pseudoinverse in cases where closed form formulas exist.
- Parameters:
y (torch.Tensor) – a measurement \(y\) to reconstruct via the pseudoinverse.
x_init (torch.Tensor) – initial guess for the reconstruction.
- Returns:
(torch.Tensor) The reconstructed image \(x\).
- A_vjp(x, v)[source]
Computes the product between a vector \(v\) and the Jacobian of the forward operator \(A\) evaluated at \(x\), defined as:
\[A_{vjp}(x, v) = \left. \frac{\partial A}{\partial x} \right|_x^\top v.\]By default, the Jacobian is computed using automatic differentiation.
- Parameters:
x (torch.Tensor) – signal/image.
v (torch.Tensor) – vector.
- Returns:
(torch.Tensor) the VJP product between \(v\) and the Jacobian.
- __add__(other)[source]
Stacks two linear forward operators \(A(x) = \begin{bmatrix} A_1(x) \\ A_2(x) \end{bmatrix}\) via the add operation.
The measurements produced by the resulting model are
deepinv.utils.TensorListobjects, where each entry corresponds to the measurements of the corresponding operator.- Parameters:
other (deepinv.physics.Physics) – Physics operator \(A_2\)
- Returns:
(deepinv.physics.Physics) stacked operator
- __mul__(other)[source]
Concatenates two forward operators \(A = A_1\circ A_2\) via the mul operation
The resulting operator keeps the noise and sensor models of \(A_1\).
- Parameters:
other (deepinv.physics.Physics) – Physics operator \(A_2\)
- Returns:
(deepinv.physics.Physics) concantenated operator
- forward(x, **kwargs)[source]
Computes forward operator
\[y = N(A(x), \sigma)\]- Parameters:
x (torch.Tensor, list[torch.Tensor]) – signal/image
- Returns:
(torch.Tensor) noisy measurements
- noise(x, **kwargs)[source]
Incorporates noise into the measurements \(\tilde{y} = N(y)\)
- Parameters:
x (torch.Tensor) – clean measurements
noise_level (None, float) – optional noise level parameter
- Return torch.Tensor:
noisy measurements
- sensor(x)[source]
Computes sensor non-linearities \(y = \eta(y)\)
- Parameters:
x (torch.Tensor,list[torch.Tensor]) – signal/image
- Returns:
(torch.Tensor) clean measurements
Examples using Physics:

Imaging inverse problems with adversarial networks

Reconstructing an image using the deep image prior.

Random phase retrieval and reconstruction methods.

Expected Patch Log Likelihood (EPLL) for Denoising and Inpainting
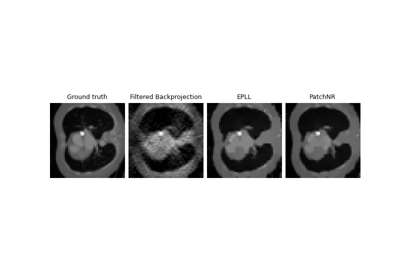
Patch priors for limited-angle computed tomography

Plug-and-Play algorithm with Mirror Descent for Poisson noise inverse problems.

Regularization by Denoising (RED) for Super-Resolution.

PnP with custom optimization algorithm (Condat-Vu Primal-Dual)

Self-supervised learning with measurement splitting
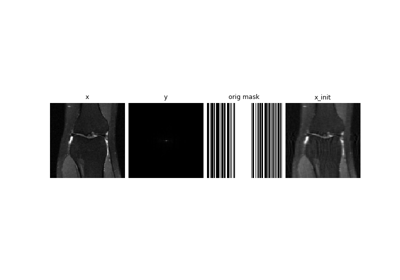
Self-supervised MRI reconstruction with Artifact2Artifact

Self-supervised denoising with the Neighbor2Neighbor loss.
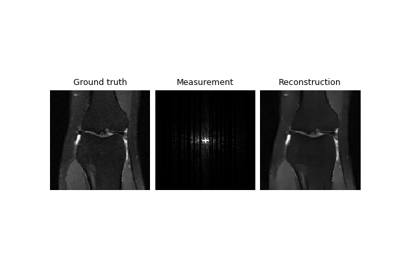
Self-supervised learning with Equivariant Imaging for MRI.

Self-supervised learning from incomplete measurements of multiple operators.

Learned Iterative Soft-Thresholding Algorithm (LISTA) for compressed sensing

Deep Equilibrium (DEQ) algorithms for image deblurring

Unfolded Chambolle-Pock for constrained image inpainting