GaussianNoise#
- class deepinv.physics.GaussianNoise(sigma=0.1, rng=None)[source]#
Bases:
NoiseModelGaussian noise \(y=z+\epsilon\) where \(\epsilon\sim \mathcal{N}(0,I\sigma^2)\).
- Parameters:
sigma (Union[float, torch.Tensor]) – Standard deviation of the noise.
rng (torch.Generator, None) – (optional) a pseudorandom random number generator for the parameter generation.
- Examples:
Adding gaussian noise to a physics operator by setting the
noise_modelattribute of the physics operator:>>> from deepinv.physics import Denoising, GaussianNoise >>> import torch >>> physics = Denoising() >>> physics.noise_model = GaussianNoise() >>> x = torch.rand(3, 1, 2, 2) >>> y = physics(x)
We can sum 2 GaussianNoise instances:
>>> gaussian_noise_1 = GaussianNoise(sigma=3.0) >>> gaussian_noise_2 = GaussianNoise(sigma=4.0) >>> gaussian_noise = gaussian_noise_1 + gaussian_noise_2 >>> y = gaussian_noise(x) >>> gaussian_noise.sigma.item() 5.0
We can also multiply a GaussianNoise by a float:
\(scaled\_gaussian\_noise(x) = \lambda \times gaussian\_noise(x)\)>>> scaled_gaussian_noise = 3.0 * gaussian_noise >>> y = scaled_gaussian_noise(x) >>> scaled_gaussian_noise.sigma.item() 15.0
We can also create a batch of GaussianNoise with different standard deviations:
\(x=[x_1, ..., x_b]\)\(t=[[[[\lambda_1]]], ..., [[[\lambda_b]]]]\) a batch of scaling factors.\([t \times gaussian](x) = [\lambda_1 \times gaussian(x_1), ..., \lambda_b \times gaussian(x_b)]\)>>> t = torch.rand((x.size(0),) + (1,) * (x.dim() - 1)) # if x.shape = (b, 3, 32, 32) then t.shape = (b, 1, 1, 1) >>> batch_gaussian_noise = t * gaussian_noise >>> y = batch_gaussian_noise(x) >>> assert (t[0]*gaussian_noise).sigma.item() == batch_gaussian_noise.sigma[0].item(), "Wrong standard deviation value for the first GaussianNoise."
- __add__(other)[source]#
Sum of 2 gaussian noises via + operator.
\(\sigma = \sqrt{\sigma_1^2 + \sigma_2^2}\)
- Parameters:
other (deepinv.physics.GaussianNoise) – Gaussian with standard deviation \(\sigma\)
- Returns:
(
deepinv.physics.GaussianNoise) – Gaussian noise with the sum of the linears operators.
- __mul__(other)[source]#
Element-wise multiplication of a GaussianNoise via
*operator.If
otheris aNoiseModel, then applies the multiplication fromNoiseModel.If
otheris afloat, then the standard deviation of the GaussianNoise is multiplied byother.\(x=[x_1, ..., x_b]\) a batch of images.\(\lambda\) a float.\(\sigma = [\lambda \times \sigma_1, ..., \lambda \times \sigma_b]\)If
otheris atorch.Tensor, then the standard deviation of the GaussianNoise is multiplied byother.\(x=[x_1, ..., x_b]\) a batch of images.\(other=[[[[\lambda_1]]], ..., [[[\lambda_b]]]]\) a batch of scaling factors.\(\sigma = [\lambda \times \sigma_1, ..., \lambda \times \sigma_b]\)
- Parameters:
other (float or torch.Tensor) – Scaling factor for the GaussianNoise’s standard deviation.
- Returns:
(
deepinv.physics.GaussianNoise) – A new GaussianNoise with the new standard deviation.
- forward(x, sigma=None, seed=None, **kwargs)[source]#
Adds the noise to measurements x
- Parameters:
x (torch.Tensor) – measurements
sigma (float, torch.Tensor) – standard deviation of the noise. If not
None, it will overwrite the current noise level.seed (int) – the seed for the random number generator, if
rngis provided.
- Returns:
noisy measurements
Examples using GaussianNoise:#

Reconstructing an image using the deep image prior.

Expected Patch Log Likelihood (EPLL) for Denoising and Inpainting
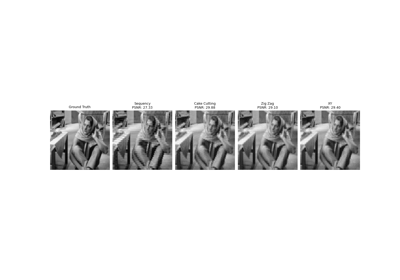
Pattern Ordering in a Compressive Single Pixel Camera

PnP with custom optimization algorithm (Primal-Dual Condat-Vu)

Regularization by Denoising (RED) for Super-Resolution.

Using state-of-the-art diffusion models from HuggingFace Diffusers with DeepInverse

Flow-Matching for posterior sampling and unconditional generation

Self-supervised denoising with the Generalized R2R loss.

Self-supervised learning with measurement splitting

Deep Equilibrium (DEQ) algorithms for image deblurring
Reducing the memory and computational complexity of unfolded network training