TomographyWithAstra#

class deepinv.physics.TomographyWithAstra(img_size, num_angles=180, num_detectors=None, angular_range=(0, torch.pi), detector_spacing=1.0, object_spacing=(1.0, 1.0), bounding_box=None, angles=None, geometry_type='parallel', geometry_parameters={'source_radius': 80.0, 'detector_radius': 20.0}, geometry_vectors=None, normalize=False, device=torch.device('cuda'), **kwargs)[source]#

Bases: LinearPhysics

Computed Tomography operator with astra-toolbox backend. It is more memory efficient than the deepinv.physics.Tomography operator and support 3D geometries. See documentation of deepinv.physics.functional.XrayTransform for more information on the astra wrapper.

Mathematically, it is described as a ray transform \(A\) which linearly integrates an object \(x\) along straight lines

\[y = \forw{x}\]

where \(y\) is the set of line integrals, called sinogram in 2D, or radiographs in 3D. An object is typically scanned using a surrounding circular trajectory. Given different acquisition systems, the lines along which the integrals are computed follow different geometries:

  • parallel. (2D and 3D)

    Per view, all rays intersecting the object are parallel. In 2D, all rays live on the same plane, perpendicular to the axis of rotation.

  • fanbeam. (2D)

    Per view, all rays come from a single source and intersect the object at a certain angle. The detector consists of a 1d line of cells. Similar to the 2D “parallel”, all rays live on the same plane, perpendicular to the axis of rotation.

  • conebeam. (3D)

    Per view, all rays come from a single source. The detector consists of a 2D grid of cells. Apart from the central plane, the set of rays coming onto a line of cells live on a tilted plane.

Note

The pseudo-inverse is computed using the filtered back-projection algorithm with a Ramp filter, and its equivalent for conebeam 3D, the Feldkamp-Davis-Kress algorithm. This is not the exact linear pseudo-inverse of the Ray Transform, but it is a good approximation which is robust to noise.

Note

In the default configuration, reconstruction cells and detector cells are set to have isotropic unit lengths. The geometry is set to 2D parallel and matches the default configuration of the deepinv.physics.Tomography operator with circle=False.

Warning

Due to computational efficiency reasons, the projector and backprojector implemented in astra are not matched. The projector is typically ray-driven, while the backprojector is pixel-driven. The adjoint of the forward Ray Transform is approximated by rescaling the backprojector.

Warning

The deepinv.physics.functional.XrayTransform used in deepinv.physics.TomographyWithAstra sequentially processes batch elements, which can make the 2D parallel beam operator significantly slower than its native torch counterpart with deepinv.physics.Tomography (though still more memory-efficient).

Parameters:

  • img_size (tuple[int, ...]) – Shape of the object grid, either a 2 or 3-element tuple, for respectively 2D or 3D.

  • num_angles (int) – Number of angular positions sampled uniformly in angular_range. (default: 180)

  • num_detectors (int | tuple[int, ...], None) – In 2D, specify an integer for a single line of detector cells. In 3D, specify a 2-element tuple for (row,col) shape of the detector. (default: None)

  • angular_range (tuple[float, float]) – Angular range, defaults to (0, torch.pi).

  • detector_spacing (float | tuple[float, float]) – In 2D the width of a detector cell. In 3D a 2-element tuple specifying the (vertical, horizontal) dimensions of a detector cell. (default: 1.0)

  • object_spacing (tuple[float, ...]) – In 2D, the (x,y) dimensions of a pixel in the reconstructed image. In 3D, the (x,y,z) dimensions of a voxel. (default: (1.,1.))

  • bounding_box (tuple[float, ...], None) – Axis-aligned bounding-box of the reconstruction area [min_x, max_x, min_y, max_y, …]. Optional argument, if specified, overrides argument object_spacing. (default: None)

  • angles (torch.Tensor, None) – Tensor containing angular positions in radii. Optional, if specified, overrides arguments num_angles and angular_range. (default: None)

  • geometry_type (str) – The type of geometry among 'parallel', 'fanbeam' in 2D and 'parallel' and 'conebeam' in 3D. (default: 'parallel')

  • geometry_parameters (dict[str, Any]) –

    Contains extra parameters specific to certain geometries. When geometry_type='fanbeam' or 'conebeam', the dictionnary should contains the keys

    • "source_radius": the distance between the x-ray source and the rotation axis, denoted \(D_{s0}\), (default: 80.),

    • "detector_radius": the distance between the x-ray detector and the rotation axis, denoted \(D_{0d}\). (default: 20.)

  • geometry_vectors (torch.Tensor, None) –

    Alternative way to describe a 3D geometry. It is a torch.Tensor of shape [num_angles, 12], where for each angular position of index i the row consists of a vector of size (12,) with

    • (sx, sy, sz): the position of the source,

    • (dx, dy, dz): the center of the detector,

    • (ux, uy, uz): the horizontal unit vector of the detector,

    • (vx, vy, vz): the vertical unit vector of the detector.

    When specified, geometry_vectors overrides detector_spacing, num_angles/angles and geometry_parameters. It is particularly useful to build the geometry for the Walnut-CBCT dataset, where the acquisition parameters are provided via such vectors.

  • normalize (bool) – If True A() and A_adjoint() are normalized so that the operator has unit norm. (default: False)

  • device (torch.device | str) – The operator only supports CUDA computation. (default: torch.device('cuda'))

Examples:

Tomography operator with a 2D 'fanbeam' geometry, 10 uniformly sampled angles in [0,2*torch.pi], a detector line of 5 cells with length 2., a source-radius of 20.0 and a detector_radius of 20.0 for 5x5 image:

 >>> from deepinv.physics import TomographyWithAstra
 >>> seed = torch.manual_seed(0)  # Random seed for reproducibility
 >>> x = torch.randn(1, 1, 5, 5, device='cuda') # Define random 5x5 image
 >>> physics = TomographyWithAstra(
 ...        img_size=(5,5),
 ...        num_angles=10,
 ...        angular_range=(0, 2*torch.pi),
 ...        num_detectors=5,
 ...        detector_spacing=2.0,
 ...        geometry_type='fanbeam',
 ...        geometry_parameters={
 ...            'source_radius': 20.,
 ...            'detector_radius': 20.
 ...        }
 ...    )
 >>> sinogram = physics(x)
 >>> print(sinogram)
 tensor([[[[-2.4262, -0.3840, -2.1681, -1.1024,  1.8009],
         [-2.4597, -0.0198, -1.6027,  0.1117,  1.0543],
         [-3.8424, -2.5034,  1.8132,  2.4666, -1.0440],
         [-3.0843, -2.0380,  2.2693,  2.4964, -2.7098],
         [ 0.6441, -2.2355, -0.2281,  0.2533, -1.3641],
         [ 1.7683, -0.9205, -2.1681, -0.2436, -2.5756],
         [ 0.4655,  0.3250, -1.6027, -0.6839, -2.4529],
         [-2.4195,  3.1875,  1.8132, -2.3952, -3.5968],
         [-1.6350,  1.4374,  2.2693, -2.2185, -3.7328],
         [-1.9789,  0.1986, -0.2281, -1.7952, -0.3667]]]], device='cuda:0')

Tomography operator with a 3D 'conebeam' geometry, 10 uniformly sampled angles in [0,2*torch.pi], a detector grid of 5x5 cells of size (2.,2.), a source-radius of 20.0 and a detector_radius of 20.0 for a 5x5x5 volume:

 >>> seed = torch.manual_seed(0)  # Random seed for reproducibility
 >>> x = torch.randn(1, 1, 5, 5, 5, device='cuda')  # Define random 5x5x5 volume
 >>> angles = torch.linspace(0, 2*torch.pi, steps=4)[:-1]
 >>> physics = TomographyWithAstra(
 ...        img_size=(5,5,5),
 ...        angles = angles,
 ...        num_detectors=(5,5),
 ...        object_spacing=(1.0,1.0,1.0),
 ...        detector_spacing=(2.0,2.0),
 ...        geometry_type='conebeam',
 ...        geometry_parameters={
 ...            'source_radius': 20.,
 ...            'detector_radius': 20.
 ...       }
 ...    )
 >>> sinogram = physics(x)
 >>> print(sinogram)
 tensor([[[[[-2.0464,  0.4064, -1.5184, -0.9225,  1.5369],
         [-2.3398, -0.9323,  2.0437,  0.5806, -1.5659],
         [-1.0852,  2.0659,  1.1105, -1.7271, -2.6104]],

         [[ 1.4757, -0.2731,  0.9386,  0.5791,  0.2995],
         [-0.8362,  2.5918,  1.0941,  1.0576, -1.4501],
         [-1.1313,  3.8354, -0.9572, -2.3721,  3.5149]],

         [[ 0.6392,  0.1564, -0.8063, -3.8958,  1.2547],
         [ 0.5294, -1.0241, -0.1792, -0.5054, -1.4253],
         [-1.1961, -1.6911,  0.4279, -1.3608,  0.9488]],

         [[ 0.5134,  2.1534, -3.8697,  0.3571,  0.1060],
         [ 0.4687, -3.0669,  1.5911,  1.5235, -0.8031],
         [-1.1990,  0.2637,  2.0889, -0.8894,  0.2550]],

         [[-1.4643, -0.2128,  1.3425,  2.8803, -0.6605],
         [ 0.9605,  1.1056,  4.2324, -3.5795, -0.1718],
         [ 0.9207,  1.6948,  1.6556, -1.6624,  0.9960]]]]], device='cuda:0')
A(x, **kwargs)[source]#

Forward projection.

Parameters:

x (torch.Tensor) – input of shape [B,C,…,H,W]

Returns:

projection of shape [B,C,…,A,N]

Return type:

Tensor

A_adjoint(y, **kwargs)[source]#

Approximation of the adjoint.

Parameters:

y (torch.Tensor) – input of shape [B,C,…,A,N]

Returns:

torch.Tensor filtered back-projection of shape [B,C,…,H,W]

Return type:

Tensor

A_dagger(y, **kwargs)[source]#

Pseudo-inverse estimated using filtered back-projection.

Parameters:

y (torch.Tensor) – input of shape [B,C,…,A,N]

Returns:

torch.Tensor filtered back-projection of shape [B,C,…,H,W]

Return type:

Tensor

fbp_weighting(sinogram)[source]#

Scales the computation by the inverse number of views and object-to-dector cell ratio.

In conebeam 3D, compute FDK weights to correct inflated distances due to tilted rays. Given coordinate \((x,y)\) of a detector cell, the corresponding weight is \(\omega(x,y) = \frac{D_{s0}}{\sqrt{D_{sd}^2 + x^2 + y^2}}\).

Parameters:

sinogram (torch.Tensor) – Sinogram of shape [B,C,…,A,N].

Returns:

Weighted sinogram.

Return type:

Tensor

Examples using TomographyWithAstra:#

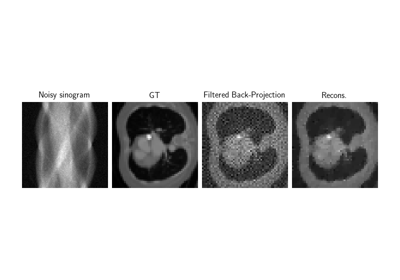
Low-dose CT with ASTRA backend and Total-Variation (TV) prior

Low-dose CT with ASTRA backend and Total-Variation (TV) prior