Potential#
- class deepinv.optim.Potential(fn=None)[source]#
Bases:
ModuleBase class for a potential \(h : \xset \to \mathbb{R}\) to be used in an optimization problem.
Comes with methods to compute the potential gradient, its proximity operator, its convex conjugate (and associated gradient and prox).
- Parameters:
fn (Callable) – Potential function \(h(x)\) to be used in the optimization problem.
- bregman_prox(x, bregman_potential, *args, gamma=1.0, stepsize_inter=1.0, max_iter_inter=50, tol_inter=1e-3, **kwargs)[source]#
Calculates the (right) Bregman proximity operator of h` at \(x\), with Bregman potential
bregman_potential.\[\operatorname{prox}^h_{\gamma \regname}(x) = \underset{u}{\text{argmin}} \frac{\gamma}{2}h(u) + D_\phi(u,x)\]where \(D_\phi(x,y)\) stands for the Bregman divergence with potential \(\phi\).
By default, the proximity operator is computed using internal gradient descent.
- Parameters:
x (torch.Tensor) – Variable \(x\) at which the proximity operator is computed.
bregman_potential (deepinv.optim.bregman.Bregman) – Bregman potential to be used in the Bregman proximity operator.
gamma (float) – stepsize of the proximity operator.
stepsize_inter (float) – stepsize used for internal gradient descent
max_iter_inter (int) – maximal number of iterations for internal gradient descent.
tol_inter (float) – internal gradient descent has converged when the L2 distance between two consecutive iterates is smaller than tol_inter.
- Returns:
(torch.Tensor) proximity operator \(\operatorname{prox}^h_{\gamma \regname}(x)\), computed in \(x\).
- conjugate(x, *args, **kwargs)[source]#
Computes the convex conjugate potential \(h^*(y) = \sup_{x} \langle x, y \rangle - h(x)\). By default, the conjugate is computed using internal gradient descent.
- Parameters:
x (torch.Tensor) – Variable \(x\) at which the conjugate is computed.
- Returns:
(torch.Tensor) conjugate potential \(h^*(y)\).
- fn(x, *args, **kwargs)[source]#
Computes the value of the potential \(h(x)\).
- Parameters:
x (torch.Tensor) – Variable \(x\) at which the potential is computed.
- Returns:
(torch.Tensor) prior \(h(x)\).
- forward(x, *args, **kwargs)[source]#
Computes the value of the potential \(h(x)\).
- Parameters:
x (torch.Tensor) – Variable \(x\) at which the potential is computed.
- Returns:
(torch.Tensor) prior \(h(x)\).
- grad(x, *args, **kwargs)[source]#
Calculates the gradient of the potential term \(h\) at \(x\). By default, the gradient is computed using automatic differentiation.
- Parameters:
x (torch.Tensor) – Variable \(x\) at which the gradient is computed.
- Returns:
(torch.Tensor) gradient \(\nabla_x h\), computed in \(x\).
- grad_conj(x, *args, **kwargs)[source]#
Calculates the gradient of the convex conjugate potential \(h^*\) at \(x\). If the potential is convex and differentiable, the gradient of the conjugate is the inverse of the gradient of the potential. By default, the gradient is computed using automatic differentiation.
- Parameters:
x (torch.Tensor) – Variable \(x\) at which the gradient is computed.
- Returns:
(torch.Tensor) gradient \(\nabla_x h^*\), computed in \(x\).
- prox(x, *args, gamma=1.0, stepsize_inter=1.0, max_iter_inter=50, tol_inter=1e-3, **kwargs)[source]#
Calculates the proximity operator of \(h\) at \(x\). By default, the proximity operator is computed using internal gradient descent.
- Parameters:
x (torch.Tensor) – Variable \(x\) at which the proximity operator is computed.
gamma (float) – stepsize of the proximity operator.
stepsize_inter (float) – stepsize used for internal gradient descent
max_iter_inter (int) – maximal number of iterations for internal gradient descent.
tol_inter (float) – internal gradient descent has converged when the L2 distance between two consecutive iterates is smaller than tol_inter.
- Returns:
(torch.Tensor) proximity operator \(\operatorname{prox}_{\gamma h}(x)\), computed in \(x\).
- prox_conjugate(x, *args, gamma=1.0, lamb=1.0, **kwargs)[source]#
Calculates the proximity operator of the convex conjugate \((\lambda h)^*\) at \(x\), using the Moreau formula.
::Warning:: Only valid for convex potential.
- Parameters:
x (torch.Tensor) – Variable \(x\) at which the proximity operator is computed.
gamma (float) – stepsize of the proximity operator.
lamb (float) – math:
lambdaparameter in front of \(f\)
- Returns:
(torch.Tensor) proximity operator \(\operatorname{prox}_{\gamma \lambda h)^*}(x)\), computed in \(x\).
Examples using Potential:#
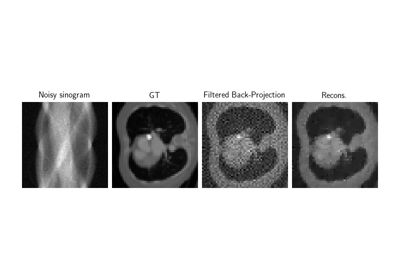
Low-dose CT with ASTRA backend and Total-Variation (TV) prior
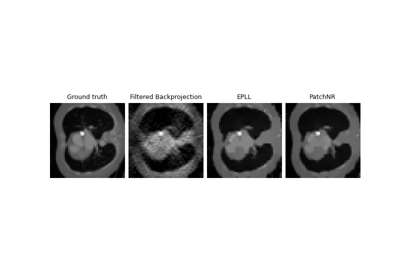
Patch priors for limited-angle computed tomography

Random phase retrieval and reconstruction methods.
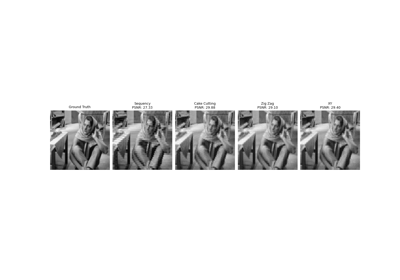
Pattern Ordering in a Compressive Single Pixel Camera

PnP with custom optimization algorithm (Primal-Dual Condat-Vu)

Plug-and-Play algorithm with Mirror Descent for Poisson noise inverse problems.

Regularization by Denoising (RED) for Super-Resolution.

Using state-of-the-art diffusion models from HuggingFace Diffusers with DeepInverse

Building your diffusion posterior sampling method using SDEs

Deep Equilibrium (DEQ) algorithms for image deblurring

Learned Iterative Soft-Thresholding Algorithm (LISTA) for compressed sensing
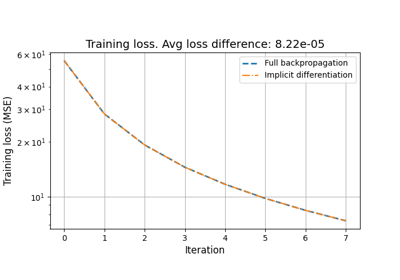
Reducing the memory and computational complexity of unfolded network training

Unfolded Chambolle-Pock for constrained image inpainting