Tomography#

class deepinv.physics.Tomography(angles, img_width, circle=False, parallel_computation=True, adjoint_via_backprop=False, fbp_interpolate_boundary=False, normalize=None, fan_beam=False, fan_parameters=None, device=torch.device('cpu'), dtype=torch.float, **kwargs)[source]#

Bases: LinearPhysics

(Computed) Tomography operator.

The Radon transform is the integral transform which takes a square image \(x\) defined on the plane to a function \(y=\forw{x}\) defined on the (two-dimensional) space of lines in the plane, whose value at a particular line is equal to the line integral of the function over that line.

Note

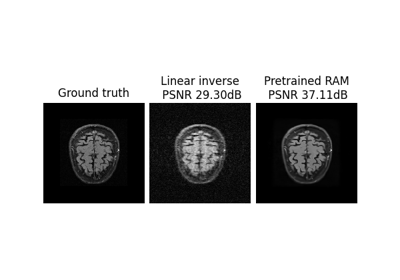
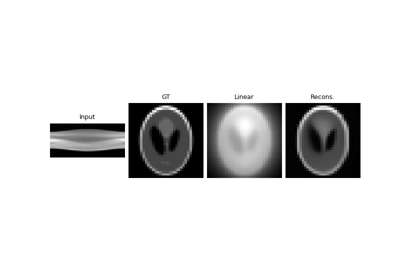
The pseudo-inverse is computed using the filtered back-projection algorithm with a Ramp filter. This is not the exact linear pseudo-inverse of the Radon transform, but it is a good approximation which is robust to noise.

Note

The measurements are not normalized by the image size, thus the norm of the operator depends on the image size.

Note

This operator only handles 2D images. For more advanced use-cases, see the deepinv.physics.TomographyWithAstra operator which handles 2D and 3D geometries.

Warning

The adjoint operator has small numerical errors due to interpolation. Set adjoint_via_backprop=True if you want to use the exact adjoint (computed via autograd).

Warning

By default, normalize is set to True if not specified. Initializing the operator without specifying the normalization behavior will issue a warning. Note that normalizing the operator affects the reconstruction dynamics, which may not always be suitable for real-world applications.

Parameters:

angles (int, torch.Tensor) – These are the tomography angles. If the type is int, the angles are sampled uniformly between 0 and 360 degrees. If the type is torch.Tensor, the angles are the ones provided (e.g., torch.linspace(0, 180, steps=10)).
img_width (int) – width/height of the square image input.
circle (bool) – If True both forward and backward projection will be restricted to pixels inside a circle inscribed in the square image.
parallel_computation (bool) – if True, all projections are performed in parallel. Requires more memory but is faster on GPUs.
adjoint_via_backprop (bool) – if True, the adjoint will be computed via deepinv.physics.adjoint_function(). Otherwise the inverse Radon transform is used. The inverse Radon transform is computationally cheaper (particularly in memory), but has a small adjoint mismatch. The backprop adjoint is the exact adjoint, but might break random seeds since it backpropagates through torch.nn.functional.grid_sample(), see the note here.
fbp_interpolate_boundary (bool) – the filtered back-projection usually contains streaking artifacts on the boundary due to padding. For fbp_interpolate_boundary=True these artifacts are corrected by cutting off the outer two pixels of the FBP and recovering them by interpolating the remaining image. This option only makes sense if circle is set to False. Hence it will be ignored if circle is True.
normalize (bool) – If True A and A_adjoint are normalized so that the operator has unit norm. (default: True)
fan_beam (bool) – If True, use fan beam geometry, if False use parallel beam
fan_parameters (dict[str, int | float]) –
Only used if fan_beam is True. Contains the parameters defining the scanning geometry. The dict should contain the keys:
- ”pixel_spacing” defining the distance between two pixels in the image, default: 0.5 / (in_size)
- ”source_radius” distance between the x-ray source and the rotation axis (middle of the image), default: 57.5
- ”detector_radius” distance between the x-ray detector and the rotation axis (middle of the image), default: 57.5
- ”n_detector_pixels” number of pixels of the detector, default: 258
- ”detector_spacing” distance between two pixels on the detector, default: 0.077
The default values are adapted from the geometry in Khalil et al.[1]. where pixel spacing, source and detector radius and detector spacing are given in cm. Note that a to small value of n_detector_pixels*detector_spacing can lead to severe circular artifacts in any reconstruction.
device (str) – gpu or cpu.

Examples:

Tomography operator with defined angles for 3x3 image:

>>> from deepinv.physics import Tomography
>>> seed = torch.manual_seed(0)  # Random seed for reproducibility
>>> x = torch.randn(1, 1, 4, 4)  # Define random 4x4 image
>>> angles = torch.linspace(0, 45, steps=3)
>>> physics = Tomography(angles=angles, img_width=4, circle=True, normalize=False)
>>> physics(x)
tensor([[[[ 0.0000, -0.1791, -0.1719],
          [-0.5713, -0.4521, -0.5177],
          [ 0.0340,  0.1448,  0.2334],
          [ 0.0000, -0.0448, -0.0430]]]])

Tomography operator with 3 uniformly sampled angles in [0, 360] for 3x3 image:

>>> from deepinv.physics import Tomography
>>> seed = torch.manual_seed(0)  # Random seed for reproducibility
>>> x = torch.randn(1, 1, 4, 4)  # Define random 4x4 image
>>> physics = Tomography(angles=3, img_width=4, circle=True, normalize=False)
>>> physics(x)
tensor([[[[ 0.0000, -0.1806,  0.0500],
          [-0.5713, -0.6076, -0.6815],
          [ 0.0340,  0.3175,  0.0167],
          [ 0.0000, -0.0452,  0.0989]]]])

References:

A(x, **kwargs)[source]#

Forward projection.

Parameters:: x (torch.Tensor) – input of shape [B,C,H,W]
Returns:: measurement of shape [B,C,A,N], with A the number of angular positions, and N the number of detector cells.
Return type:: Tensor

A_adjoint(y, **kwargs)[source]#

Computes adjoint of the tomography operator.

Warning

The default adjoint operator has small numerical errors due to interpolation. Set adjoint_via_backprop=True if you want to use the exact adjoint (computed via autograd).

Parameters:: y (torch.Tensor) – measurements of shape [B,C,A,N]
Returns:: scaled back-projection of shape [B,C,H,W]
Return type:: Tensor

A_dagger(y, **kwargs)[source]#

Computes the filtered back-projection (FBP) of the measurements.

Warning

The filtered back-projection algorithm is not the exact linear pseudo-inverse of the Radon transform, but it is a good approximation that is robust to noise.

Tip

By default, the FBP reconstruction can display artifacts at the borders. Set fbp_interpolate_boundary=True to remove them with padding.

Parameters:: y (torch.Tensor) – measurements of shape [B,C,A,N], with A the number of angular positions, and N the number of detector cells
Returns:: filtered back-projection of shape [B,C,H,W]
Return type:: Tensor

Examples using `Tomography`:#

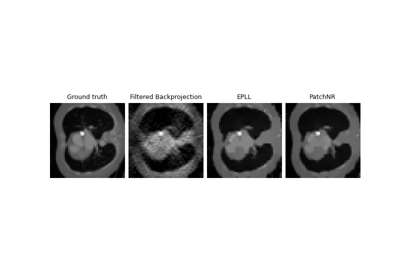
Inference and fine-tune a foundation model

Patch priors for limited-angle computed tomography

Tour of forward sensing operators

Vanilla PnP for computed tomography (CT).

Self-supervised learning with measurement splitting

Learned Primal-Dual algorithm for CT scan.

Tomography#

Examples using Tomography:#

This Page

Examples using `Tomography`:#