DecomposablePhysics#
- class deepinv.physics.DecomposablePhysics(U=None, V_adjoint=None, img_size=None, U_adjoint=None, V=None, mask=1.0, **kwargs)[source]#
Bases:
LinearPhysicsParent class for linear operators with SVD decomposition.
The singular value decomposition is expressed as
\[A = U\text{diag}(s)V^{\top} \in \mathbb{R}^{m\times n}\]where \(U\in\mathbb{C}^{n\times n}\) and \(V\in\mathbb{C}^{m\times m}\) are orthonormal linear transformations and \(s\in\mathbb{R}_{+}^{n}\) are the singular values.
- Parameters:
U (None | Callable) – orthonormal transformation. If
None(default), it is set to the identity function.V_adjoint (None | Callable) – transpose of V. If
None(default), it is set to the identity function.img_size (tuple) – (optional, only required if V and/or U_adjoint are not provided) size of the signal/image
x, e.g.(C, ...)whereCis the number of channels and...are the spatial dimensions, used for the automatic adjoint computation.U_adjoint (None | Callable) – transpose of U. If
None(default), it is computed automatically usingdeepinv.physics.adjoint_function()from theUfunction and theimg_sizeparameter. This automatic adjoint is computed using automatic differentiation, which is slower than a closed form adjoint, and can have a larger memory footprint. If you want to use the automatic adjoint, you should set theimg_sizeparameter.V (None | Callable) – If
None(default), it is computed automatically usingdeepinv.physics.adjoint_function()from theV_adjointfunction and theimg_sizeparameter. This automatic adjoint is computed using automatic differentiation, which is slower than a closed form adjoint, and can have a larger memory footprint. If you want to use the automatic adjoint, you should set theimg_sizeparameter.params (torch.nn.parameter.Parameter, float) – Singular values of the transform
- Examples:
Recreation of the Inpainting operator using the DecomposablePhysics class:
>>> from deepinv.physics import DecomposablePhysics >>> seed = torch.manual_seed(0) # Random seed for reproducibility >>> img_size = (1, 1, 3, 3) # Input size >>> mask = torch.tensor([[1, 0, 1], [1, 0, 1], [1, 0, 1]]) # Binary mask >>> U = lambda x: x # U is the identity operation >>> U_adjoint = lambda x: x # U_adjoint is the identity operation >>> V = lambda x: x # V is the identity operation >>> V_adjoint = lambda x: x # V_adjoint is the identity operation >>> mask_svd = mask.float().unsqueeze(0).unsqueeze(0) # Convert the mask to torch.Tensor and adjust its dimensions >>> physics = DecomposablePhysics(U=U, U_adjoint=U_adjoint, V=V, V_adjoint=V_adjoint, mask=mask_svd)
Apply the operator to a random tensor:
>>> x = torch.randn(img_size) >>> with torch.no_grad(): ... physics.A(x) # Apply the masking tensor([[[[ 1.5410, -0.0000, -2.1788], [ 0.5684, -0.0000, -1.3986], [ 0.4033, 0.0000, -0.7193]]]])
- A(x, mask=None, **kwargs)[source]#
Applies the forward operator \(y = A(x)\).
If a mask/singular values is provided, it is used to apply the forward operator, and also stored as the current mask/singular values.
- Parameters:
x (torch.Tensor) – input tensor
mask (torch.nn.parameter.Parameter, float) – singular values.
- Returns:
output tensor
- Return type:
- A_A_adjoint(y, mask=None, **kwargs)[source]#
A helper function that computes \(A A^{\top}y\).
Using the SVD decomposition, we have \(A A^{\top} = U\text{diag}(s^2)U^{\top}\).
- Parameters:
y (torch.Tensor) – measurement.
- Returns:
(
torch.Tensor) the product \(AA^{\top}y\).
- A_adjoint(y, mask=None, **kwargs)[source]#
Computes the adjoint of the forward operator \(\tilde{x} = A^{\top}y\).
If a mask/singular values is provided, it is used to apply the adjoint operator, and also stored as the current mask/singular values.
- Parameters:
y (torch.Tensor) – input tensor
mask (torch.nn.parameter.Parameter, float) – singular values.
- Returns:
output tensor
- Return type:
- A_adjoint_A(x, mask=None, **kwargs)[source]#
A helper function that computes \(A^{\top} A x\).
Using the SVD decomposition, we have \(A^{\top}A = V\text{diag}(s^2)V^{\top}\).
- Parameters:
x (torch.Tensor) – signal/image.
- Returns:
(
torch.Tensor) the product \(A^{\top}Ax\).
- A_dagger(y, mask=None, **kwargs)[source]#
Computes \(A^{\dagger}y = x\) in an efficient manner leveraging the singular vector decomposition.
- Parameters:
y (torch.Tensor) – a measurement \(y\) to reconstruct via the pseudoinverse.
- Returns:
(
torch.Tensor) The reconstructed image \(x\).
- U(x)[source]#
Applies the \(U\) operator of the SVD decomposition.
Note
This method should be overwritten by the user to define its custom
DecomposablePhysicsoperator.- Parameters:
x (torch.Tensor) – input tensor
- U_adjoint(x, **kwargs)[source]#
Applies the \(U^{\top}\) operator of the SVD decomposition.
Note
This method should be overwritten by the user to define its custom
DecomposablePhysicsoperator.- Parameters:
x (torch.Tensor) – input tensor
- V(x, **kwargs)[source]#
Applies the \(V\) operator of the SVD decomposition.
Note
This method should be overwritten by the user to define its custom
DecomposablePhysicsoperator.- Parameters:
x (torch.Tensor) – input tensor
- V_adjoint(x)[source]#
Applies the \(V^{\top}\) operator of the SVD decomposition.
Note
This method should be overwritten by the user to define its custom
DecomposablePhysicsoperator.- Parameters:
x (torch.Tensor) – input tensor
- prox_l2(z, y, gamma, **kwargs)[source]#
Computes proximal operator of \(f(x)=\frac{\gamma}{2}\|Ax-y\|^2\) in an efficient manner leveraging the singular vector decomposition.
- Parameters:
z (torch.Tensor, float) – signal tensor
y (torch.Tensor) – measurements tensor
gamma (float) – hyperparameter \(\gamma\) of the proximal operator
- Returns:
(
torch.Tensor) estimated signal tensor
Examples using DecomposablePhysics:#

Reconstructing an image using the deep image prior.

Expected Patch Log Likelihood (EPLL) for Denoising and Inpainting
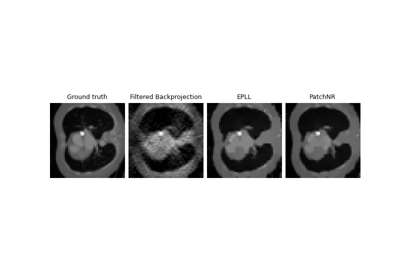
Patch priors for limited-angle computed tomography
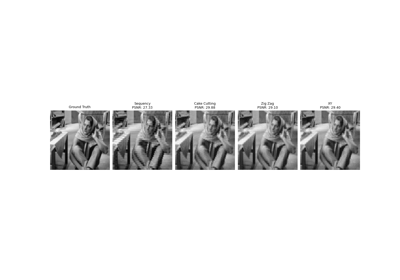
Pattern Ordering in a Compressive Single Pixel Camera

PnP with custom optimization algorithm (Primal-Dual Condat-Vu)

Plug-and-Play algorithm with Mirror Descent for Poisson noise inverse problems.

Using state-of-the-art diffusion models from HuggingFace Diffusers with DeepInverse

Building your diffusion posterior sampling method using SDEs
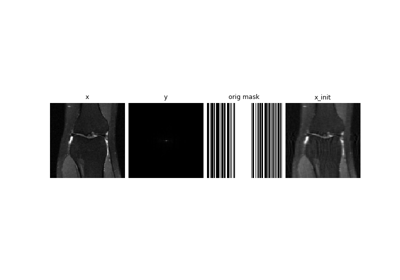
Self-supervised MRI reconstruction with Artifact2Artifact
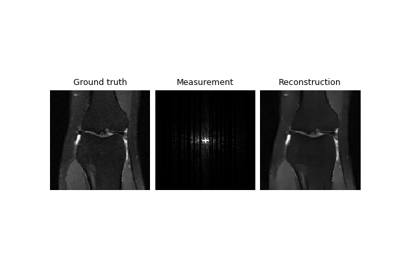
Self-supervised learning with Equivariant Imaging for MRI.

Self-supervised learning from incomplete measurements of multiple operators.

Self-supervised denoising with the Neighbor2Neighbor loss.

Self-supervised denoising with the Generalized R2R loss.

Deep Equilibrium (DEQ) algorithms for image deblurring
Reducing the memory and computational complexity of unfolded network training

Unfolded Chambolle-Pock for constrained image inpainting