R2RLoss#

class deepinv.loss.R2RLoss(metric: Metric | Module = MSELoss(), noise_model: NoiseModel = GaussianNoise(), alpha=0.5, sigma=None, eval_n_samples=5)[source]#

Bases: Loss

Generalized Recorrupted-to-Recorrupted (GR2R) Loss

This loss can be used for unsupervised image denoising with unorganized noisy images, where the noise model \(y\sim p(y\vert x)\) belongs to the exponential family as:

\[p(y\vert x) = h(x) \exp \left( y^\top \eta(x) - \phi(x) \right),\]

which includes the popular Gaussian, Poisson and Gamma noise distributions (see https://en.wikipedia.org/wiki/Exponential_family for more details on the exponential family). For this family of noisy measurements, we genealize the corruption strategy as:

\[y_1 \sim p(y_1 \vert y, \alpha ),\]
\[y_2 = \frac{1}{\alpha} \left( y - y_1(1-\alpha) \right),\]

then, the loss is computed as:

\[\| AR(y_1) - y_2 \|_2^2,\]

where, \(R\) is the trainable network, \(A\) is the forward operator, \(y\) is the noisy measurement, and \(\alpha\) is a scaling factor.

The loss was first introduced in the Recorrupted2Recorrupted paper for the specific case of Gaussian noise, formalizing the Noise2Noisier loss such that it is statistically equivalent to the supervised loss function defined on noisy/clean image pairs. The loss was later extended to other exponential family noise distributions in Generalized Recorrupted2Recorrupted paper, including Poisson, Gamma and Binomial noise distributions.

Warning

The model should be adapted before training using the method adapt_model() to include the additional noise at the input.

Note

To obtain the best test performance, the trained model should be averaged at test time over multiple realizations of the added noise, i.e. \(\hat{x} = \frac{1}{N}\sum_{i=1}^N R(y_1^{(i)})\), where \(N>1\). This can be achieved using adapt_model().

Deprecated since version 0.2.3: The sigma paramater is deprecated and will be removed in future versions. Use noise_model=deepinv.physics.GaussianNoise(sigma=sigma) parameter instead.

Parameters:

Example:

>>> import torch
>>> import deepinv as dinv
>>> sigma = 0.1
>>> noise_model = dinv.physics.GaussianNoise(sigma)
>>> physics = dinv.physics.Denoising(noise_model)
>>> model = dinv.models.MedianFilter()
>>> loss = dinv.loss.R2RLoss(noise_model=noise_model, eval_n_samples=2)
>>> model = loss.adapt_model(model) # important step!
>>> x = torch.ones((1, 1, 8, 8))
>>> y = physics(x)
>>> x_net = model(y, physics, update_parameters=True) # save extra noise in forward pass
>>> l = loss(x_net, y, physics, model)
>>> print(l.item() > 0)
True
adapt_model(model, **kwargs)[source]#

Adds noise to model input.

This method modifies a reconstruction model \(R\) to include the re-corruption mechanism at the input:

\[\hat{R}(y) = \frac{1}{N}\sum_{i=1}^N R(y_1^{(i)}),\]

where \(y_1^{(i)} \sim p(y_1 \vert y, \alpha)\) are i.i.d samples, and \(N\geq 1\) are the number of samples used for the Monte Carlo approximation. During training (i.e. when model.train()), we use only one sample, i.e. \(N=1\) for computational efficiency, whereas at test time, we use multiple samples for better performance.

Parameters:
Returns:

(torch.nn.Module) Modified model.

forward(x_net, y, physics, model, **kwargs)[source]#

Computes the GR2R Loss.

Parameters:
Returns:

(torch.Tensor) R2R loss.

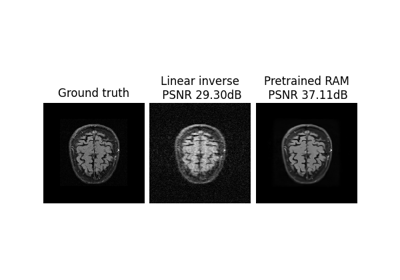
Examples using R2RLoss:#

Self-supervised denoising with the Generalized R2R loss.

Self-supervised denoising with the Generalized R2R loss.