SplittingLoss#

class deepinv.loss.SplittingLoss(metric=torch.nn.MSELoss(), split_ratio=0.9, mask_generator=None, eval_n_samples=5, eval_split_input=True, eval_split_output=False, pixelwise=True, normalize_loss=True)[source]#

Bases: Loss

Measurement splitting loss.

Implements measurement splitting loss. Splits the measurement and forward operator \(A\) (of size \(m\)) into two smaller pairs \((y_1,A_1)\) (of size \(m_1\)) and \((y_2,A_2)\) (of size \(m_2\)) , to compute the self-supervised loss:

\[\frac{m}{m_2}\| y_2 - A_2 \inversef{y_1}{A_1}\|^2\]

where \(R\) is the trainable network, \(A_1 = M_1 A, A_2 = M_2 A\), and \(M_i\) are randomly generated masks (i.e. diagonal matrices) such that \(M_1+M_2=\mathbb{I}_m\).

See Self-supervised learning with measurement splitting for usage example.

Note

If the forward operator has its own subsampling mask \(M_{A}\), e.g. deepinv.physics.Inpainting or deepinv.physics.MRI, the splitting masks will be subsets of the physics’ mask such that \(M_1+M_2=M_{A}\)

This loss was used for MRI in Yaman et al. Self-supervised learning of physics-guided reconstruction neural networks without fully sampled reference data (SSDU) for MRI, Hendriksen et al. (Noise2Inverse) for CT, as well as numerous other papers. Note we use implement the multi-mask strategy proposed by Yaman et al..

By default, the error is computed using the MSE metric, however any appropriate metric can be used.

Warning

The model should be adapted before training using the method adapt_model to include the splitting mechanism at the input.

Note

To obtain the best test performance, the trained model should be averaged at test time over multiple realizations of the splitting, i.e. \(\hat{x} = \frac{1}{N}\sum_{i=1}^N \inversef{y_1^{(i)}}{A_1^{(i)}}\). To disable this, set eval_n_samples=1.

Note

To disable measurement splitting (and use the full input) at evaluation time, set eval_split_input=False. This is done in SSDU.

See also

deepinv.loss.mri.Artifact2ArtifactLoss, deepinv.loss.mri.Phase2PhaseLoss, deepinv.loss.mri.WeightedSplittingLoss, deepinv.loss.mri.RobustSplittingLoss: Specialised splitting losses and their extensions for MRI applications.

Parameters:

metric (Metric, torch.nn.Module) – metric used for computing data consistency, which is set as the mean squared error by default.
split_ratio (float) – splitting ratio, should be between 0 and 1. The size of \(y_1\) increases with the splitting ratio. Ignored if mask_generator passed.
mask_generator (deepinv.physics.generator.BernoulliSplittingMaskGenerator, None) – function to generate the mask. If None, the deepinv.physics.generator.BernoulliSplittingMaskGenerator is used, with the parameters split_ratio and pixelwise.
eval_n_samples (int) – Number of samples used for averaging at evaluation time. Must be greater than 0.
eval_split_input (bool) – if True, perform input measurement splitting during evaluation. If False, use full measurement at eval (no MC samples are performed and eval_split_output will have no effect)
eval_split_output (bool) – at evaluation time, pass the output through the output mask too. i.e. \((\sum_{j=1}^N M_2^{(j)})^{-1} \sum_{i=1}^N M_2^{(i)} \inversef{y_1^{(i)}}{A_1^{(i)}}\). Only valid when \(y\) is same domain (and dimension) as \(x\). Although better results may be observed on small datasets, more samples must be used for bigger images. Defaults to False.
pixelwise (bool) – if True, create pixelwise splitting masks i.e. zero all channels simultaneously. Ignored if mask_generator passed.
normalize_loss (bool) – whether to normalize loss by the target size

Example:

>>> import torch
>>> import deepinv as dinv
>>> physics = dinv.physics.Inpainting(img_size=(1, 8, 8), mask=0.5)
>>> model = dinv.models.MedianFilter()
>>> loss = dinv.loss.SplittingLoss(split_ratio=0.9, eval_n_samples=2)
>>> model = loss.adapt_model(model) # important step!
>>> x = torch.ones((1, 1, 8, 8))
>>> y = physics(x)
>>> x_net = model(y, physics, update_parameters=True) # save random mask in forward pass
>>> l = loss(x_net, y, physics, model)
>>> print(l.item() > 0)
True

class SplittingModel(model, split_ratio, mask_generator, eval_n_samples, eval_split_input, eval_split_output, pixelwise)[source]#

Bases: Reconstructor

Model wrapper when using SplittingLoss.

Performs input splitting during forward pass. At evaluation, perform forward passes for multiple realisations of splitting mask and average.

Parameters:

model (deepinv.models.Reconstructor) – base model
split_ratio (float) – splitting ratio, should be between 0 and 1. The size of \(y_1\) increases with the splitting ratio. Ignored if mask_generator passed.
mask_generator (deepinv.physics.generator.PhysicsGenerator, None) – function to generate the mask. If None, the deepinv.physics.generator.BernoulliSplittingMaskGenerator is used, with the parameters split_ratio and pixelwise.
eval_n_samples (int) – Number of samples used for averaging at evaluation time. Must be greater than 0.
eval_split_input (bool) – if True, perform input measurement splitting during evaluation. If False, use full measurement at eval (no MC samples are performed and eval_split_output will have no effect)
eval_split_output (bool) – at evaluation time, pass the output through the output mask too. i.e. \((\sum_{j=1}^N M_2^{(j)})^{-1} \sum_{i=1}^N M_2^{(i)} \inversef{y_1^{(i)}}{A_1^{(i)}}\). Only valid when \(y\) is same domain (and dimension) as \(x\). Although better results may be observed on small datasets, more samples must be used for bigger images. Defaults to False.
pixelwise (bool) – if True, create pixelwise splitting masks i.e. zero all channels simultaneously. Ignored if mask_generator passed.

forward(y, physics, update_parameters=False)[source]#

Adapted model forward pass for input splitting. During training, only one splitting realisation is performed for computational efficiency.

static split(mask, y, physics=None)[source]#

Perform splitting given mask

Parameters:

mask (torch.Tensor) – splitting mask
y (torch.Tensor) – input data
physics (deepinv.physics.Physics) – physics to split, retaining its original noise model. If None, only \(y\) is split.

adapt_model(model, eval_n_samples=None)[source]#

Apply random splitting to input.

This method modifies a reconstruction model \(R\) to include the splitting mechanism at the input:

\[\hat{R}(y, A) = \frac{1}{N}\sum_{i=1}^N \inversef{y_1^{(i)}}{A_1^{(i)}}\]

where \(N\geq 1\) is the number of Monte Carlo samples, and \(y_1^{(i)}\) and \(A_1^{(i)}\) are obtained by randomly splitting the measurements \(y\) and operator \(A\). During training (i.e. when model.train()), we use only one sample, i.e. \(N=1\) for computational efficiency, whereas at test time, we use multiple samples for better performance. For other parameters that control how splitting is applied, see the class parameters.

Parameters:

model (torch.nn.Module) – Reconstruction model.
eval_n_samples (int) – deprecated. Pass eval_n_samples at class initialisation instead.

Returns:

(torch.nn.Module) Model modified for evaluation.

Return type:

SplittingModel

forward(x_net, y, physics, model, **kwargs)[source]#

Computes the measurement splitting loss

Parameters:

x_net (torch.Tensor) – reconstructions.
y (torch.Tensor) – Measurements.
physics (deepinv.physics.Physics) – Forward operator associated with the measurements.
model (torch.nn.Module) – Reconstruction function.

Returns:

(torch.Tensor) loss.

static split(mask, y, physics=None)[source]#

Perform splitting given mask

Parameters:

mask (torch.Tensor) – splitting mask of shape (B,C,H,W)
y (torch.Tensor) – input data of shape (B,C,…,H,W)
physics (deepinv.physics.Physics) – physics to split, retaining its original noise model. If None, only \(y\) is split.

Examples using `SplittingLoss`:#

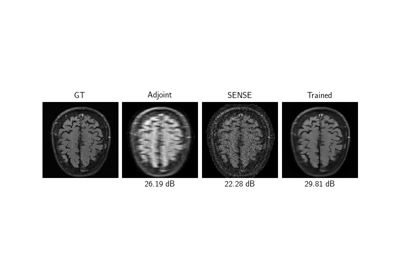
Self-supervised MRI reconstruction with Artifact2Artifact

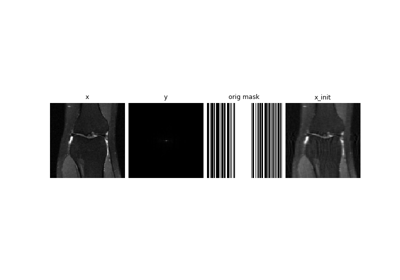
Self-supervised learning with measurement splitting

SplittingLoss#

Examples using SplittingLoss:#

This Page

Examples using `SplittingLoss`:#