EILoss#
- class deepinv.loss.EILoss(transform, metric=None, apply_noise=True, weight=1.0, no_grad=False, *args, **kwargs)[source]#
Bases:
LossEquivariant imaging self-supervised loss.
Assumes that the set of signals is invariant to a group of transformations (rotations, translations, etc.) in order to learn from incomplete measurement data alone. The EI loss, as proposed by Chen et al.[1], is defined as
\[\| T_g \hat{x} - \inverse{\forw{T_g \hat{x}}}\|^2\]where \(\hat{x}=\inverse{y}\) is a reconstructed signal and \(T_g\) is a transformation sampled at random from a group \(g\sim\group\).
By default, the error is computed using the MSE metric, however any other metric (e.g., \(\ell_1\)) can be used as well.
- Parameters:
transform (deepinv.transform.Transform) – Transform to generate the virtually augmented measurement. It can be any torch-differentiable function (e.g., a
torch.nn.Module) including torchvision transforms.metric (Metric, torch.nn.Module) – Metric used to compute the error between the reconstructed augmented measurement and the reference image.
apply_noise (bool) – if
True, the augmented measurement is computed with the full sensing model \(\sensor{\noise{\forw{\hat{x}}}}\) (i.e., noise and sensor model), otherwise is generated as \(\forw{\hat{x}}\).weight (float) – Weight of the loss.
no_grad (bool) – if
True, the gradient does not propagate through \(T_g\). Default:False. This option is useful for super-resolution problems, see Scanvic et al.[2] for details.
- References:
- forward(x_net, physics, model, **kwargs)[source]#
Computes the EI loss
- Parameters:
x_net (torch.Tensor) – Reconstructed image \(\inverse{y}\).
physics (deepinv.physics.Physics) – Forward operator associated with the measurements.
model (torch.nn.Module) – Reconstruction function.
- Returns:
(
torch.Tensor) loss.
Examples using EILoss:#
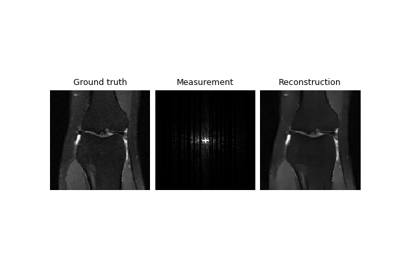
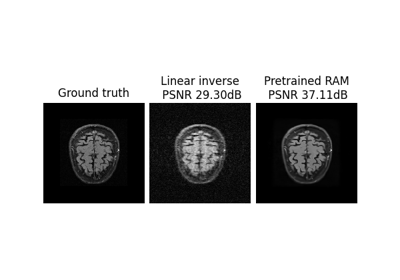
Self-supervised learning with Equivariant Imaging for MRI.